【智能算法应用】徒步优化算法求解二维路径规划问题

摘要
本文提出了一种基于徒步优化算法的二维路径规划方法,用于解决机器人在平面空间中寻找最优路径的问题。该算法模仿徒步旅行者在复杂地形中寻找最佳路线的过程,通过反复调整路径和评估各路径的代价来获得全局最优解。实验结果表明,徒步优化算法能够有效避开障碍物,并在较短的迭代次数内快速收敛,找到路径代价最低的解。
理论
-
徒步优化算法简介: 徒步优化算法是一种启发式优化算法,灵感来自于人在徒步旅行中逐步寻找最优路径的过程。在算法中,每个解代表一个徒步者的当前路径位置,徒步者通过评估当前位置的代价逐步朝向较优路径移动,直到找到全局最优路径。
-
二维路径规划: 该算法用于在二维空间中进行路径规划,目标是从起点到达终点,路径中需避开障碍物并使路径代价最小化。路径的代价由路径长度和路径中的障碍物位置共同决定。徒步者通过反复评估路径的代价并根据优化准则选择路径,逐渐收敛到全局最优解。
实验结果
-
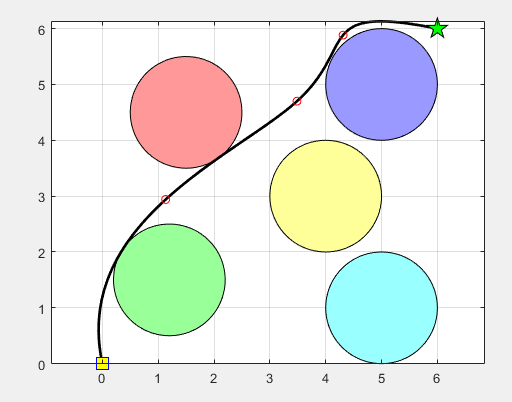
图1: 显示了徒步优化算法应用于二维路径规划的结果。红色的圆形代表障碍物,路径从起点(左下角黄色方块)到终点(右上角绿色五角星),黑色线表示通过徒步算法计算得到的最优路径。可以看到,路径成功绕过了障碍物。
-
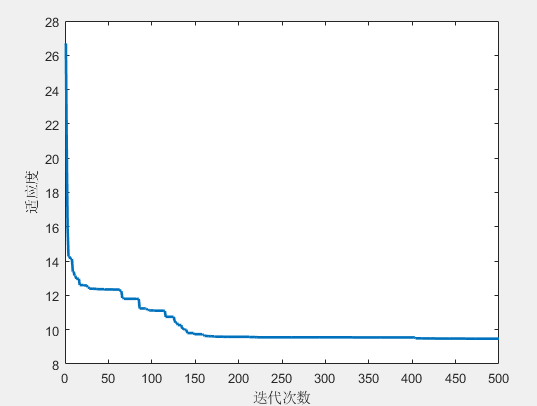
图2: 该图展示了徒步算法在多次迭代中的收敛情况。横轴表示迭代次数,纵轴表示适应度值。随着迭代次数的增加,适应度值迅速下降并趋于稳定,表明算法能够快速找到接近最优的解。
部分代码
% 参数设置
num_hikers = 30; % 徒步者数量
max_iterations = 500; % 最大迭代次数
learning_rate = 0.1; % 徒步者移动的步长% 初始化徒步者位置
positions = rand(num_hikers, 2) * 10; % 在10x10范围内随机生成位置
best_position = positions(1, :); % 记录最优位置
best_cost = inf; % 初始化最优代价为无穷大% 路径规划主循环
for iter = 1:max_iterationsfor hiker = 1:num_hikers% 计算当前路径的代价current_position = positions(hiker, :);current_cost = calculatePathCost(current_position);% 更新最优解if current_cost < best_costbest_cost = current_cost;best_position = current_position;end% 徒步者移动:朝着当前最优解方向移动positions(hiker, :) = positions(hiker, :) + learning_rate * (best_position - current_position);end
end% 代价计算函数
function cost = calculatePathCost(position)% 根据路径长度及障碍物分布计算路径代价cost = norm(position);
end
参考文献
❝
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, 4, 1942-1948.
Dehuri, S., Cho, S. B., Ghosh, A., & Ghosh, A. (2013). Swarm intelligence for multi-objective optimization. Studies in Computational Intelligence, 439, 91-118.
Back, T. (1996). Evolutionary Algorithms in Theory and Practice. Oxford University Press.
(文章内容仅供参考,具体效果以图片为准)
