代码随想录算法训练营day53：图04：104.建造最大岛屿；110. 字符串接龙；105.有向图的完全可达性

104.建造最大岛屿

卡码网题目链接（ACM模式）(opens new window)

题目描述：

给定一个由 1（陆地）和 0（水）组成的矩阵，你最多可以将矩阵中的一格水变为一块陆地，在执行了此操作之后，矩阵中最大的岛屿面积是多少。

岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。

输入描述：

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述：

输出一个整数，表示最大的岛屿面积。如果矩阵中不存在岛屿，则输出 0。

分析：

本题的一个暴力想法，应该是遍历地图尝试 将每一个 0 改成1，然后去搜索地图中的最大的岛屿面积。

计算地图的最大面积：遍历地图 + 深搜岛屿，时间复杂度为 n * n。

（其实使用深搜还是广搜都是可以的，其目的就是遍历岛屿做一个标记，相当于染色，那么使用哪个遍历方式都行，以下我用深搜来讲解）

每改变一个0的方格，都需要重新计算一个地图的最大面积，所以 整体时间复杂度为：n^4。

优化思路

其实每次深搜遍历计算最大岛屿面积，我们都做了很多重复的工作。

只要用一次深搜把每个岛屿的面积记录下来就好。

第一步：一次遍历地图，得出各个岛屿的面积，并做编号记录。可以使用map记录，key为岛屿编号，value为岛屿面积

第二步：再遍历地图，遍历0的方格（因为要将0变成1），并统计该1（由0变成的1）周边岛屿面积，将其相邻面积相加在一起，遍历所有 0 之后，就可以得出 选一个0变成1 之后的最大面积。

拿如下地图的岛屿情况来举例： （1为陆地）

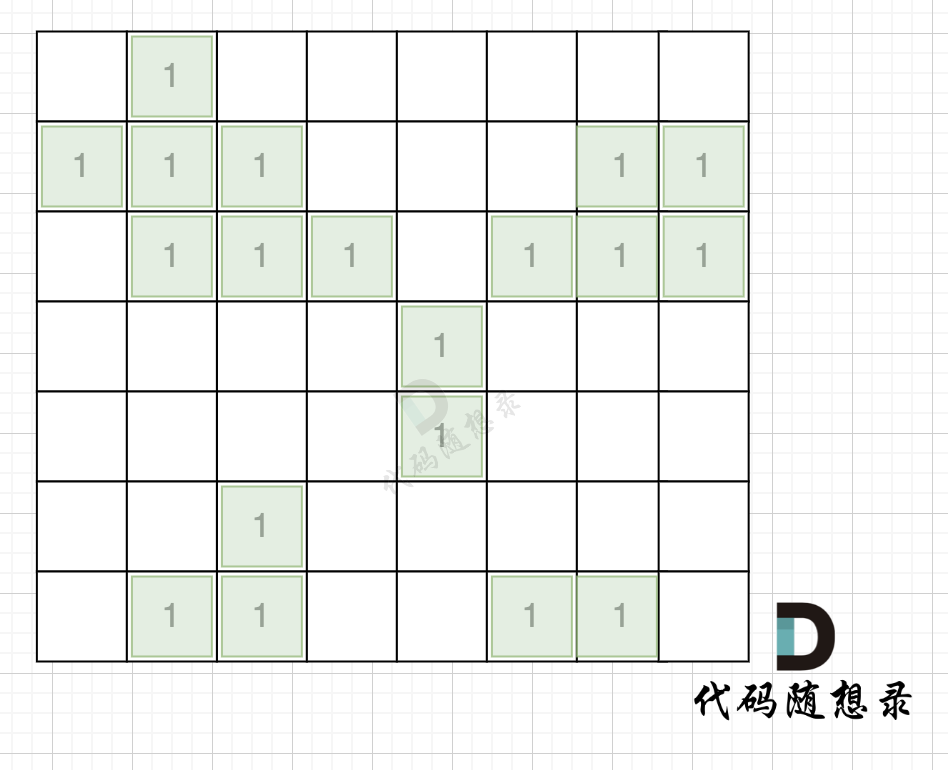
第一步，则遍历题目，并将岛屿到编号和面积上的统计，过程如图所示：

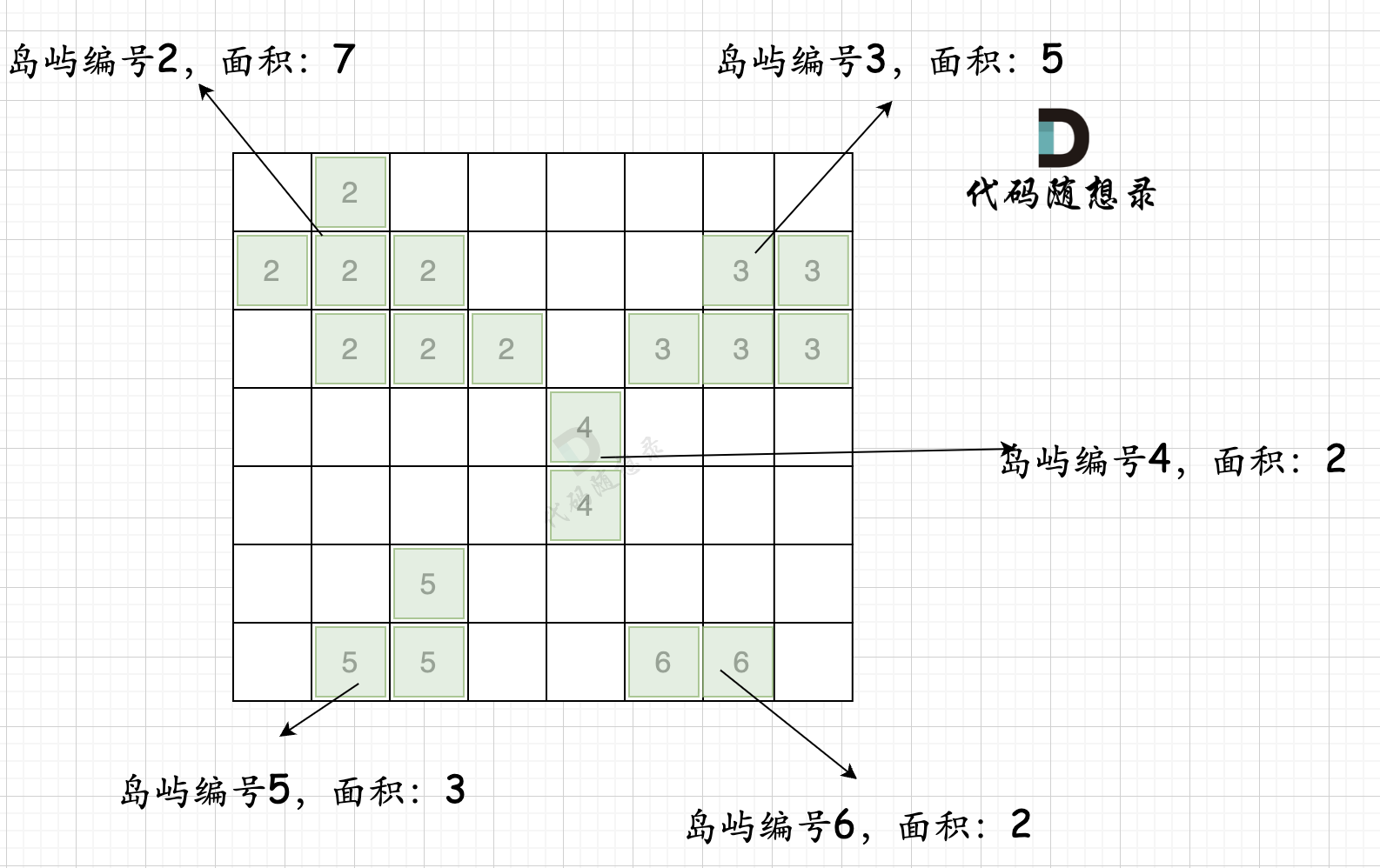
这个过程时间复杂度 n * n 。

相当于对整个矩阵深搜一遍：n*n（之前是对每个结点改变的情况，都要对整个矩阵进行深搜n^4）

再遍历空白位置：n*n

n * n这个方格地图中，每个节点我们就遍历一次，并不会重复遍历。

第二步过程如图所示：

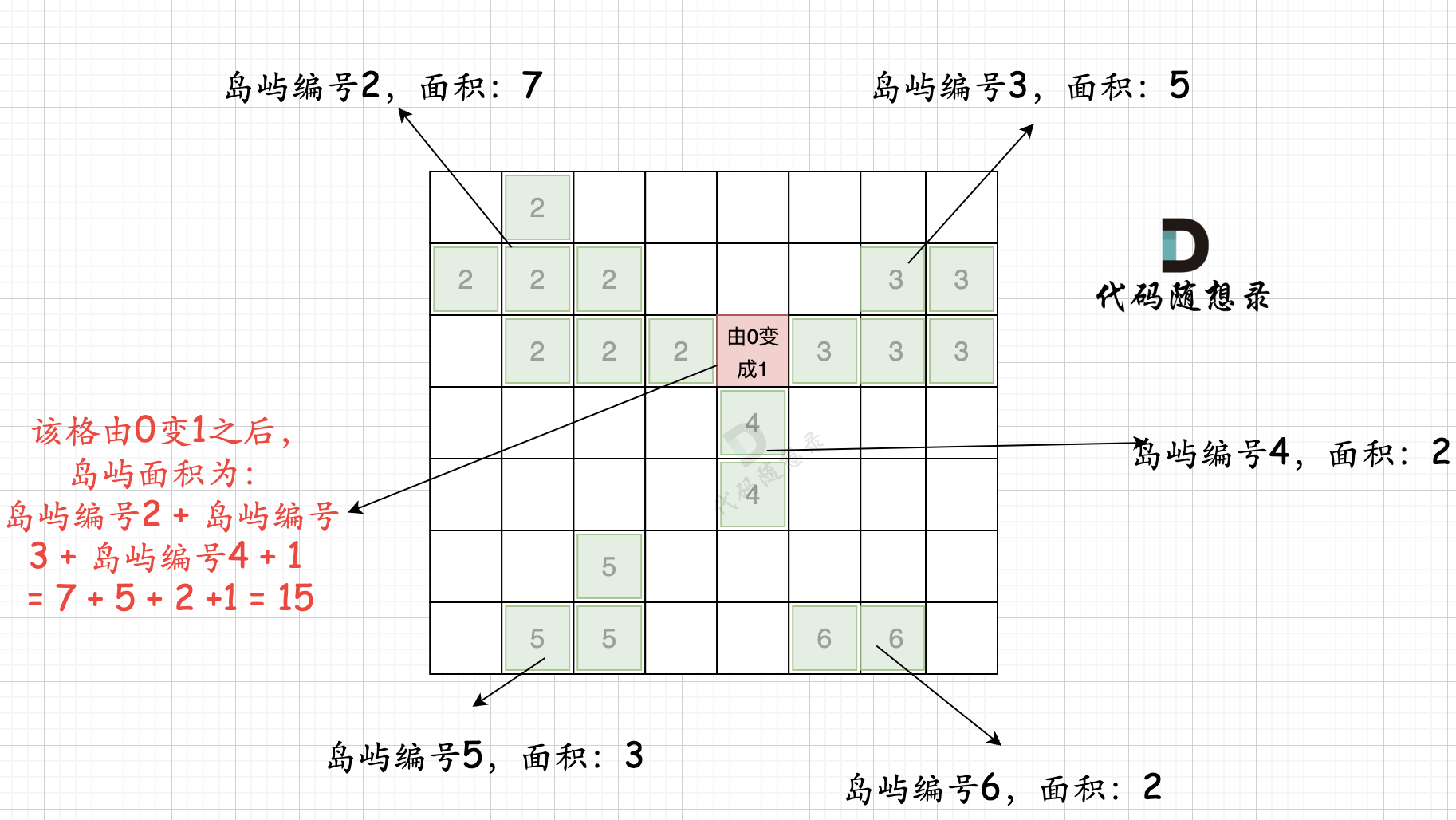
也就是遍历每一个0的方格，并统计其相邻岛屿面积，最后取一个最大值。

这个过程的时间复杂度也为 n * n。

所以整个解法的时间复杂度，为 n * n + n * n 也就是 n^2。

可以优化掉visit函数，第一个岛编号从2开始就行了，也就是已经遇到过的陆地编号不会是1，更不会是0

#include <stdio.h> 
#include <stdlib.h> 
#include <stdbool.h>
#include <string.h>
#include <math.h>int this_size,zonal_size;
int s=2;int move[4][2]={1,0,0,1,-1,0,0,-1};void dfs(int i,int j,int**box,int m,int n){box[i][j]=s;this_size++;for(int k=0;k<4;k++){int movei=i+move[k][0];int movej=j+move[k][1];if(movei>=0 && movej>=0 && movei<n && movej<m && box[movei][movej]==1) dfs(movei,movej,box,m,n);}
}void dfs2(int i,int j,int **box,int m,int n,int *copysize){//i,j附近的有编号的内容，然后加起来，然后返回for(int k=0;k<4;k++){int movei=i+move[k][0];int movej=j+move[k][1];if(movei>=0 && movej>=0 && movei<n && movej<m && box[movei][movej]!=0 && copysize[box[movei][movej]]!=0){zonal_size+= copysize[box[movei][movej]];//标记这个面积已经使用过了copysize[box[movei][movej]]=0;dfs2(movei,movej,box,m,n,copysize);}}
}int main(){int n,m;scanf("%d%d",&n,&m);int x=m*n/2+3;int** box=(int**)malloc(sizeof(int*)*n);int *size = (int*)malloc(sizeof(int)*x);for (int i=0;i<n;i++){box[i]=(int*)malloc(sizeof(int)*m);for(int j=0;j<m;j++) scanf("%d",&box[i][j]);  }for(int i=0;i<x;i++) size[i]=0;int ansmax=0;for (int i=0;i<n;i++){//统计各个岛的面积for(int j=0;j<m;j++){if(box[i][j]==1){//=1是未访问过的this_size=0;dfs(i,j,box,m,n);size[s]=this_size;s++;}}}for(int i=2;i<s;i++) ansmax=fmax(size[i],ansmax);int *copysize=(int *)malloc(sizeof(int)*x);memcpy(copysize,size,sizeof(int)*x);for (int i=0;i<n;i++){for(int j=0;j<m;j++){if(box[i][j]==0){zonal_size=1;memcpy(copysize,size,sizeof(int)*x);dfs2(i,j,box,m,n,copysize);ansmax=fmax(ansmax,zonal_size);}              }}printf("%d",ansmax);return 0;}

105.有向图的完全可达性

卡码网题目链接（ACM模式）(opens new window)

【题目描述】

给定一个有向图，包含 N 个节点，节点编号分别为 1，2，...，N。现从 1 号节点开始，如果可以从 1 号节点的边可以到达任何节点，则输出 1，否则输出 -1。

【输入描述】

第一行包含两个正整数，表示节点数量 N 和边的数量 K。 后续 K 行，每行两个正整数 s 和 t，表示从 s 节点有一条边单向连接到 t 节点。

【输出描述】

如果可以从 1 号节点的边可以到达任何节点，则输出 1，否则输出 -1。

分析：

1、用邻接表处理

2、实际上就是从1开始搜索，能到达的节点都用visit标为1

3、搜索完毕，如果有visit是0，那么就print -1；其他情况print 1

#include <stdio.h> 
#include <stdlib.h> 
#include <stdbool.h>
#include <string.h>
#include <math.h>int visited[100];
//int record[100];typedef struct arcnode{int node;struct arcnode * nextnode;
}Arcnode;typedef struct vnode{Arcnode* firstarc;
}Vnode;typedef struct {Vnode list[100];
}graph;void dfs(int x,graph *g){visited[x]=1;Arcnode*p=g->list[x].firstarc;while(p!=NULL){int w=p->node;if(visited[w]==0){dfs(w,g);}p=p->nextnode;}
}int main(){int n,k;scanf("%d%d",&n,&k);graph *g =(graph*)malloc(sizeof(graph));for(int i=1;i<=n;i++){g->list[i].firstarc=NULL;}for(int i=0;i<k;i++){int s,t;scanf("%d%d",&s,&t);Arcnode* zzz=(Arcnode*)malloc(sizeof(Arcnode));zzz->node=t;zzz->nextnode=g->list[s].firstarc;g->list[s].firstarc=zzz;}dfs(1,g);for(int i=1;i<=n;i++){if(visited[i]==0) {printf("0");return 0;}}printf("1");return 0;
}

bfs:

int queue[1000];
int front=-1,rear=-1;void bfs(int x,graph*g){queue[++rear]=x;visited[x]=1;while(front!=rear){front++;int xxx=queue[front];Arcnode*p=g->list[xxx].firstarc;while(p!=NULL){int w=p->node;if(visited[w]==0){queue[++rear]=w;visited[w]=1;}p=p->nextnode;}}
}

106. 岛屿的周长

卡码网题目链接（ACM模式）(opens new window)

题目描述

给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。

你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿，假设组成岛屿的陆地边长都为 1，请计算岛屿的周长。岛屿内部没有水域。

输入描述

第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。

输出描述

输出一个整数，表示岛屿的周长。

分析：

1、涉及到周围，附近——用bfs

2、一个陆地，有四条边，每和一个陆地相邻 就需要-1（不考虑是否visit）；但是bfs遍历的过程中 需要visit

#include <stdio.h> 
#include <stdlib.h> 
#include <stdbool.h>
#include <string.h>
#include <math.h>int rear=-1,front=-1;
int queue[100][100];
int c=0;
int count=0;int move[4][2]={1,0,0,1,-1,0,0,-1};void bfs(int**box,int i,int j,int n,int m,int **visited){rear++;queue[rear][0]=i;queue[rear][1]=j;visited[i][j]=1;while(front!=rear){front++;int xi = queue[front][0];int xj = queue[front][1];//相当于是在出队的时候，操作了count=4;for(int k=0;k<4;k++){int final_i=xi+move[k][0];int final_j=xj+move[k][1];if(final_i>=0 && final_i<n && final_j>=0 && final_j<m && box[final_i][final_j]==1) count--;if(final_i>=0 && final_i<n && final_j>=0 && final_j<m && box[final_i][final_j]==1 && visited[final_i][final_j]==0 ){rear++;queue[rear][0]=final_i;queue[rear][1]=final_j;visited[final_i][final_j]=1;}//else if(final_i>=0 && final_i<n && final_j>=0 && final_j<m && box[final_i][final_j]==0) count++;}c=c+count;}}int main(){int n,m;scanf("%d%d",&n,&m);int **box=(int**)malloc(sizeof(int*)*n);int **visited=(int**)malloc(sizeof(int*)*n);for(int i=0;i<n;i++){box[i]=(int*)malloc(sizeof(int)*m);visited[i]=(int*)malloc(sizeof(int)*m);for(int j=0;j<m;j++){scanf("%d",&box[i][j]);visited[i][j]=0;}}int p,q;int flag=1;for(int i=0;i<n && flag==1;i++){for(int j=0;j<m;j++){if(box[i][j]==1) {p=i;q=j;flag=0;break;}}}bfs(box,p,q,n,m,visited);printf("%d",c);return 0;
}

实际上不用bfs也行：

计算出总的岛屿数量，总的变数为：岛屿数量 * 4

因为有一对相邻两个陆地，边的总数就要减2，如图红线部分，有两个陆地相邻，总边数就要减2

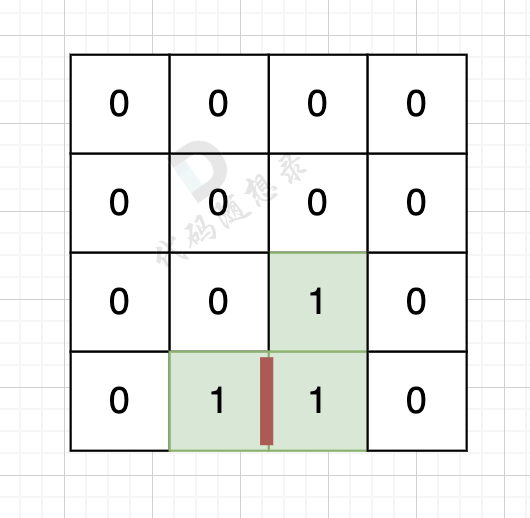
那么只需要在计算出相邻岛屿的数量就可以了，相邻岛屿数量为cover。

结果 result = 岛屿数量 * 4 - cover * 2;