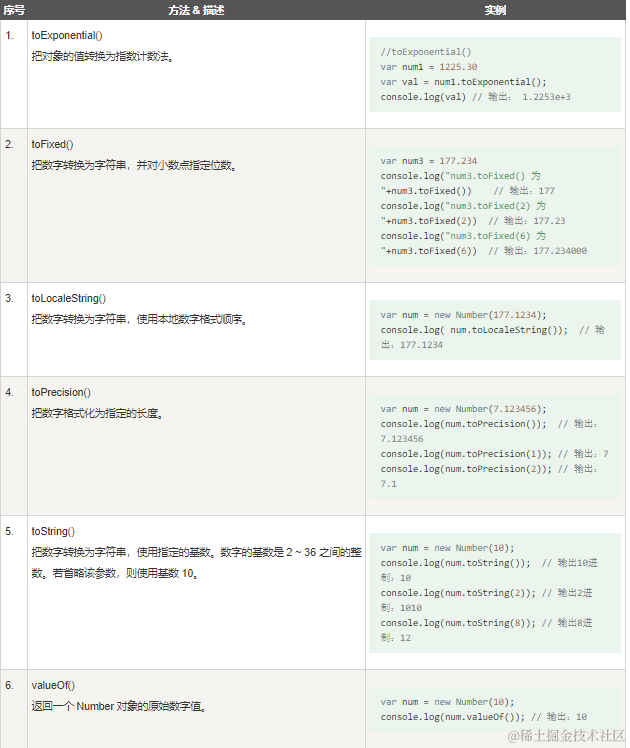
本篇文章适合个人复习翻阅，不建议新手入门使用

定义：导数
设 $f$ 是定义在区间 $I\subset R$ 上的实值函数，$x_0\in I$ 是一个给定的点，若极限
$$\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$存在，则称 $f$ 在 $x_0$ 处可导，记极限为 $f^{\prime }(x_0)$，算子记法为 $\frac{\mathrm{d}f}{\mathrm{d}x}(x_0)$
并记 $$f(x_0+h)=f(x_0)+f^{\prime }(x_0)h+o(h)$$

性质

1. 可导一定连续，连续不一定可导
2. 四则运算：设 $f,g$ 在 $(a,b)$ 上有定义且在 $x_0\in (a,b)$ 处可导，则

• $f\pm g$ 在 $x_0$ 处可导且 $(f\pm g{)}^{\prime }(x_0)=f^{\prime }(x_0)\pm g^{\prime }(x_0)$
• $f\cdot g$ 在 $x_0$ 处可导且 $(f\cdot g{)}^{\prime }(x_0)=f^{\prime }(x_0)g(x_0)+f(x_0)g^{\prime }(x_0)$
• 若 $g(x_0)\ne 0$，那么 $\frac{f}{g}$ 在 $x_0$ 处可微且 $(\frac{f}{g}{)}^{\prime }(x_0)=\frac{f^{\prime }(x_0)g(x_0)-f(x_0)g^{\prime }(x_0)}{g(x_0{)}^2}$

定义：左导数、右导数
左导数：$$f^{\prime }(x_0^{-})=\underset{h\to 0^{-}}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$
右导数：$$f^{\prime }(x_0^{+})=\underset{h\to 0^{+}}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$

性质
$f$ 在 $x_0$ 处可导，当且仅当 $f$ 在 $x_0$ 处左、右导数存在且相等

定理：链式法则
设 $\mathbb{R}$ 上的区间 $I,J$，实值函数 $f:I\to J,g:J\to \mathbb{R}$，若 $f$ 在 $x_0$ 处可导，$g$ 在 $f(x_0)$ 处可导，则复合函数 $g\circ f$ 在 $x_0$ 处可导，且$$(g\circ f{)}^{\prime }(x_0)=g^{\prime }(f(x_0))f^{\prime }(x_0)$$

定理：Leibniz公式
设 $f,g$ 是 $\mathbb{R}$ 上定义的两个 $n$ 次可导的实值函数，则
$$(f\cdot g{)}^{(n)}(x)=\sum _{k=0}^n{C}_n^k{f}^{(k)}(x)g^{(n-k)}(x)$$

证明思路：数学归纳法

定义：微分
设 $f$ 在 $x_0$ 处可导，若要用线性映射 $L:\mathbb{R}\to \mathbb{R}$ 所定义的 $L(x-x_0)$ 在 $x_0$ 附近来逼近 $f(x)-f(x_0)$，那么函数 $l:h\mapsto f^{\prime }(x_0)h$ 是最好的线性逼近，记线性映射 $$df(x_0):T_{x_0}\mathbb{R}\to T_{f(x_0)}\mathbb{R},h\mapsto f^{\prime }(x_0)h$$

则称 $df(x_0)$ 是 $f$ 在 $x_0$ 处的微分

证明思路
若另设映射 $l^{\prime }(h)=ah$，用 $l$ 和 $l^{\prime }$ 在 $x_0$ 的局部上逼近 $f(x)-f(x_0)$，由导数的定义
$$f(x)-f(x_0)-l(x-x_0)=o(1)h$$$$f(x)-f(x_0)-l^{\prime }(x-x_0)=(f^{\prime }(x_0)-a)h+o(1)h$$

令 $h=x-x_0$，则有
$$\underset{h\to 0}{\lim }\frac{E_2(h)}{E_1(h)}=\underset{h\to 0}{\lim }\frac{(f^{\prime }(x_0)-a)h+o(1)h}{h}=+\infty$$

命题
$I\subset \mathbb{R}$ 是开区间，$f:I\to \mathbb{R}$ 在 $x_0$ 处可微且 $f(x_0)\ne 0$，若设 $f^{\prime }(x_0)>0$，则存在 $x_0$ 的开邻域 $U=(x_0-\epsilon ,x_0+\epsilon )$，使得

1. 对任意 $x\in U,x>x_0$，有 $f(x)>f(x_0)$
2. 对任意 $x\in U,x<x_0$，有 $f(x)<f(x_0)$

证明思路
由导数定义，取 $\epsilon =\frac{f^{\prime }(x_0)}{2}$，则由 $|\frac{f(x)-f(x_0)}{x-x_0}-f^{\prime }(x_0)|<\frac{1}{2}{f}^{\prime }(x_0)$ 得到
$$\frac{f(x)-f(x_0)}{x-x_0}>\frac{1}{2}{f}^{\prime }(x_0)>0$$

推论
$I\subset \mathbb{R}$ 是开区间，$f:I\to \mathbb{R}$ 在 $I$ 上可微且对任意 $x\in I,f^{\prime }(x)>0$，则 $f$ 是 $I$ 上严格递增的函数

即使函数 $f$ 在点 $x_0$ 处的导数大于零，也不能推出存在该点的邻域 $U$，使得 $f$ 在这个邻域上是递增的
反例
$$f(x)=\{\begin{array}{ll}x+2x^2\sin \frac{1}{x},& x\ne 0\\ 0,& x=0\end{array}$$

可证 $f$ 在 $x=0$ 处存在导数且大于零，但对任意的 $\epsilon >0$，$f$ 在 $(-\epsilon ,\epsilon )$ 上不单调；即是说这个反例在 $x=0$ 附近振荡足够快

定义：极值
设 $f:I\to \mathbb{R},x_0\in I$，如果存在 $x_0$ 的小邻域 $U\subset I$，使得 $f(x_0)$ 是函数 $f$ 在 $U$ 上的最大值，则称 $x_0$ 是 $f$ 的一个局部极大值，类似可定义局部最小值

定理
设 $f$ 是 $I$ 上的可微函数且 $f$ 在 $x_0\in I$ 处是局部极大（极小）值，那么 $f^{\prime }(x_0)=0$

证明思路
反证法易证

参考书：

• 《数学分析》陈纪修 於崇华 金路
• 《数学分析之课程讲义》清华大学数学系及丘成桐数学中心
• 《数学分析习题课讲义》谢惠民 恽自求 易法槐 钱定边 著