【极速前进】20240804：Case2Code提升归纳推理能力、归纳推理和演绎推理、LLM Patch-level训练、LLM内部冲突和上下文冲突

相关博客
【极速前进】20240804：Case2Code提升归纳推理能力、归纳推理和演绎推理、LLM Patch-level训练、LLM内部冲突和上下文冲突
【极速前进】20240706-24240714：用于Agent的树搜、理解LLM的语种困惑、事实知识抽取微调、Quiet-STaR
【极速前进】20240615-20240623：Zipper融合模态、VideoLLM视频理解、WebAgent可以自我改善、Nemotron-4、AnyGPT统一模态
【极速前进】20240608-20240610：评估模型Prometheus 2、CoPE、DITTO：使用示例反馈对齐LLM、CoA：利用多Agent解决长文本、Qwen2在线合并优化器
【极速前进】20240524-20240526：Meta多模态模型Chameleon、参数高效微调MoRA、跨层注意力降低KV Cache、Octopus v4、SimPO
【极速前进】20240423-20240428：Phi-3、fDPO、TextSquare多模态合成数据、遵循准则而不是偏好标签、混合LoRA专家
【极速前进】20240422：预训练RHO-1、合成数据CodecLM、网页到HTML数据集、MLLM消融实验MM1、Branch-Train-Mix
【极速前进】20240415-20240421：TR-DPO、压缩与智能的线性关系、模拟伪代码改善算术能力、Many-shot、合成数据综述

一、Case2Code：利用合成数据学习归纳推理

论文名称：Case2Code: Learning Inductive Reasoning with Synthetic Data

论文地址：https://arxiv.org/pdf/2407.12504

1. 简介

• 大多数LLM擅长演绎(deductive)推理，例如CoT等；
• 本文希望探索LLM的归纳推理能力，即LLM通过示例样本来推断潜在的规则；
• 提出Case2Code任务并利用合成数据探索归纳推理能力；
• 实验显示，通过合成的归纳推理代码数据不但能够提高Case2Code任务上的效果，而且也能增强LLM的代码能力；

2. 方法

​ 问题形式化。对于一个程序$\mathcal{P}$，有$n$个输入-输出样本构成的集合${\mathcal{S}}_{\mathcal{P}}=\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$，其中$y_i=\mathcal{P}(x_i),i=1,2,\dots ,n$。Case2Code的目标是实现程序${\mathcal{P}}^{\prime }$，其能够基于输入-输出样例${\mathcal{S}}_{\mathcal{P}}$来捕获程序$\mathcal{P}$的功能。对于任意新的输入$x_{\text{new}}\notin {\mathcal{S}}_{\mathcal{P}}$，实现的程序${\mathcal{P}}^{\prime }$应该满足$\mathcal{P}(x_{\text{new}})={\mathcal{P}}^{\prime }(x_{\text{new}})$。

​ 框架概览。目标是自动化生产大规模且多样的Case2Code数据。先基于规则过滤来收集多样性的程序。利用LLM构造样本输入，并利用代码解释器生成输出。最终，基于输出过滤低质量程序，并转换为三元组(program,inputs,outputs)。

​ 收集程序。从TheStack中采样有效的Python函数。

​ 生成输入。在收集大规模函数后，接下来就是获得对应的输入和输出。利用LLM为每个函数生成合适的输入样例。

​ 获得输出。在获得高质量程序和输入，可以利用代码解释器获得输出。由于LLM生成的输入可能包含错误，利用规则和返回的输出过滤无效的输入和函数。

​ 后处理。最后的步骤是将函数和对应的输入-输出转换为Case2Code风格数据。对于一个给定的函数$\mathcal{P}$和$n$个测试用例${\mathcal{S}}_{\mathcal{P}}=\{(x_1,y_1),\dots ,(x_n,y_n)\}$。随机采样$m$个样例作为观测集${\mathcal{S}}_{\mathcal{P}}^{\prime }$。利用LLM在${\mathcal{S}}_{\mathcal{P}}^{\prime }$上执行归纳推理来重构给定的函数$\mathcal{P}$。

3. 实验

​ 总计构造了130万的数据，留出500条进行评估。实验分为三种训练变体：(1) 直接微调；(2) 混合预训练；(3) 混合微调。

上表了各个baseline模型在代码基准和Case2Code任务上的表现。代码能力越强，在Case2Code任务上的效果越好。

使用Case2Code数据微调模型后，不但在Case2Code任务是有显著改善，且对于其他代码任务也有显著提高。

二、归纳还是演绎？重新思考LLM的推理能力

论文名称：Inductive or Deductive? Rethinking the Fundamental Reasoning Abilities of LLMs

论文地址：https://arxiv.org/pdf/2408.00114

1. 简介

​ 推理包含两种类型：演绎(deductive)推理和归纳(inductive)推理。大多数LLM的推理研究都没有清晰区分演绎和归纳两种推理。那么LLM更擅长演绎推理还是归纳推理？演绎推理在LLM已经有比较多的研究，但是归纳推理没有被充分探索。为了深入研究LLM的归纳推理能力，提出了框架SolverLearner。该框架可以使LLM学习到将输入(x)映射至输出(y)的映射。研究发现，基于SolverLearner，LLM展现了卓越的归纳推理能力，在大多数样例中ACC接近于1。令人惊奇的是，尽管LLM有很强的归纳推理能力，但是缺乏演绎推理能力，特别是反事实推理。

2. 任务定义

​ 演绎和归纳推理之间的主要区别为是否为模型提供输入-输出映射。正式来说，可以描述映射为函数$f_w:X\to Y$，其中输入$x\in X$被转换为输出$y\in Y$。区别演绎和归纳推理如下：

• 演绎推理：给模型直接提供输入-输出映射，即$f_w$；
• 归纳推理：仅向模型提供少量的输入-输出样例，而不提供映射；

上图1分别展示了演绎推理(deductive)和归纳(inductive)推理。

3. 归纳推理框架：SolverLearner

​ SolverLearner仅使用in-context让LLM来学习映射函数，其包含两个阶段：

• 函数生成：该阶段提出一个能将输入数据映射为输出的函数；
• 函数执行：该阶段通过代码解释器执行函数。

4. 任务

​ 算术。两位数加法任务，研究多个数字基数，特别是8,9,10,11和16。其中基数10对应于预训练中常见的情况。在演绎推理中，显式提供基数但不提供样例，期望LLM依靠固有的演绎推理能力进行加法运算。在归纳推理中，仅提供一些few-shot的样例并需要推理出基数，然后生成求解问题的函数。

​ 基本句法推理。目标是使用人工构造的英语句子来评估LLM，这些句子不同于传统的主谓宾单词序列。对于演绎推理，向LLM提供新的词序，然后让其识别其中的主语、动词和宾语。在归纳推理中，不提供精确的词序变化指令，而是提供标准词序和修改后的词序。LLM被期望学习词序的特定改变，然后应用该规则来确定主语、动词和宾语。

​ 空间推理。略

​ 密码解密。略

5. 结果

• LLM表现出较差的演绎推理能力，特别是“反事实”任务中；
• 通过SolverLearner，LLM展现出卓越的归纳推理能力；
• 对于LLM，演绎推理比归纳推理更具有挑战性；

三、Patch级别的LLM训练

论文名称：Patch-Level Training For Large Language Models

论文地址：https://arxiv.org/pdf/2407.12665

1. 简介

​ 目前token-level训练取得了巨大的成功，但是由于需要处理大量的token，导致计算成本非常高。本文提出patch-level训练，通过将多个token压缩至单个patch来缩减序列长度。在patch-level训练中，将较短的patch序列送入模型，然后训练其预测下一个patch。随后，模型继续token-level训练来对齐推理过程。实验显示，patch-level训练能够降低整体训练成本的0.5倍，且没有对模型性能具有损害。

2. Patch-level训练

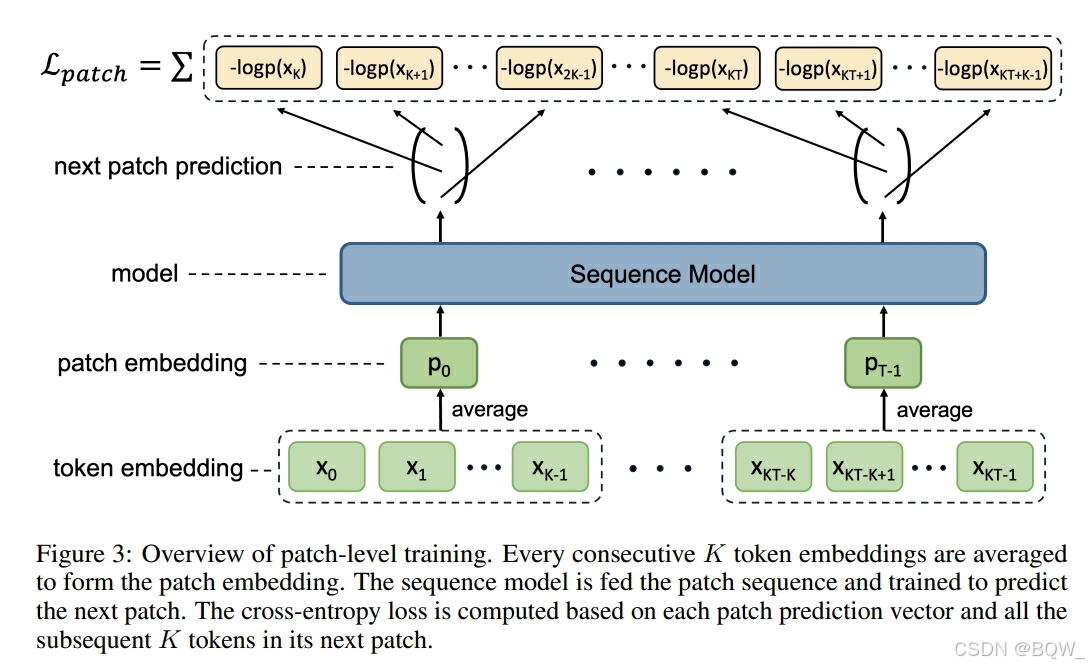
​ 将每K个连续tokens压缩至单个patch，从而实现token序列到patch序列的转变。patch序列被送入至序列模型，然后模型被训练来预测下一个patch的所有tokens。在patch-level训练中获得的知识随后被转移至token-level模型中。具体来说，使用patch-level模型获得的参数来初始化token-level模型，然后余下数据进行token-level训练。

​ 在设计patch-level模型结构时，目标是最小化patch-level和token-level模型之间的差异，确保patch-level训练获得的知识能够平滑迁移到token-level模型中。对于上下文长度为T的token-level训练，设置patch-level训练的上下文长度为KT，然后将其压缩为长度为T的patch序列，以保持随后token-level训练的一致性。为了避免在token-to-patch压缩中引入不必要的参数，patch embedding为关联token embedding的平均值。令$p_i$是第i个patch，$x_{iK+k}$是第$i$个patch中的第$k$个token，$E$是embedding函数。patch embedding为
$$\begin{gathered} E(p_i)=\frac{1}{K}\sum _{k=0}^{K-1}E(x_{iK+k}) \\ \text{\hspace{1em}(1)} \end{gathered}$$
​ patch-level模型是通过next patch预测进行训练，即预测下一个patch的K个token。在投机解码中探索了多token同步预测，其利用多个输出头且每个头负责预测单独的token。然而，该方法也包含额外的参数，这些参数对随后的知识迁移不利。相反，这里使用单独的输出头来预测下一个patch中的所有tokens。具体来说，基于相同patch预测后续$K$个tokens的交叉熵损失函数，损失函数为：
$$\begin{gathered} {\mathcal{L}}_{patch}=-\sum _{i=1}^T\sum _{k=0}^{K-1}\log p_{\theta }(x_{iK+k}|p_{<i}) \\ \text{\hspace{1em}(2)} \end{gathered}$$
因为模型最终要以token-level进行工作，为了使得patch-level模型适用token-level，保留了一些训练数据。具体来说，在训练数据中的部分$\lambda$中进行patch-level训练，然后使用参数来初始化token-level模型。随后，token-level模型继续在剩余数据上进行训练。当训练数据有限，该方法可以进行多epoch训练。例如，给定N个epoch的预算，可以在前$N\lambda$个epoch上执行patch-level训练，然后在余下的$N(1-\lambda )$个epoch上进行token-level训练。

3. 实验

3.1 设置

​ 数据集。使用包含360B token的Pile数据集。

​ 模型。采用类似于LLaMA的结构。

​ 实现细节。patch size K为4。token-level训练的上下文长度为2048。对于patch-level训练，上下文长度是K*2048。

3.2 主要结果

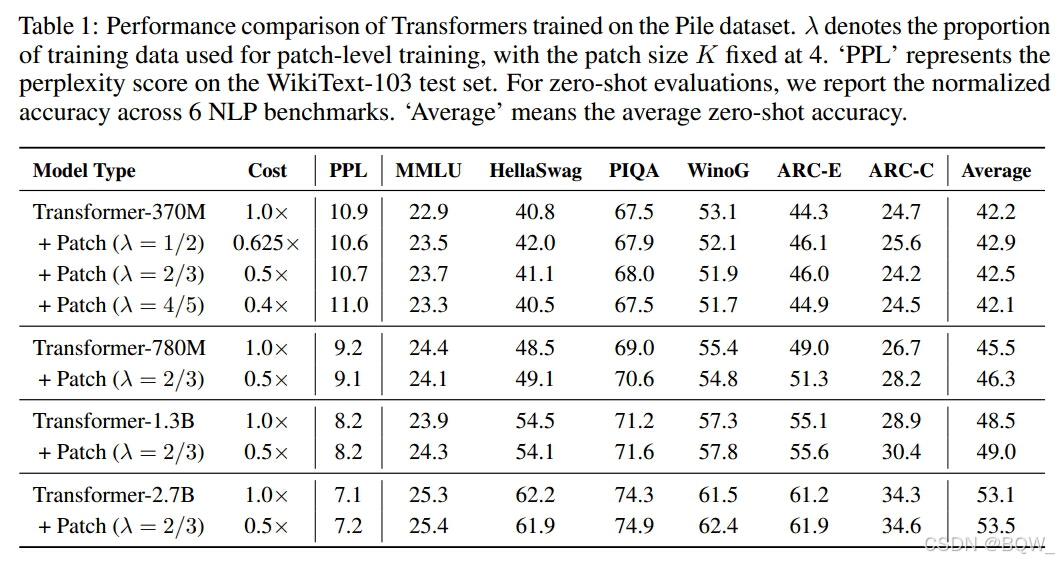
​ Patch-level训练不影响模型性能且降低训练成本。

​ 指令遵循能力类似于原始模型。

四、语言模型的内部冲突和上下文适应

论文名称：From Internal Conflict to Contextual Adaptation of Language Models

论文地址：https://arxiv.org/pdf/2407.17023

1. 简介

​ 知识密集型语言理解人物需要语言模型集成相关上下文，缓解其本身的弱点，例如不完整或者过时的知识。然而，研究表明LM经常忽略提供的上下文，因为其与预训练过程中存储在LM参数中的知识冲突。此外，冲突的知识可能已经在LM的参数中，称为intra-memory冲突。现有的工作独立研究两种类型的冲突。本文猜测intra-memory冲突可能会反过来影响LM对上context-memory冲突的影响。为了研究这个问题，引入了DYNAMICQA数据集，其包含具有时间动态性质的事实(随着时间频率的变化而变化)和有争议动态的事实(随观点而变化)。利用提出的数据集，评估衡量intra-memory的不确定性，并引入Coherent Persuasion(CP)分数来评估上下文影响LM输出的能力。实验表明，相对于时序事实和争议事实，不太可能改变的静态事实更容易用额外的使用额外的上下文更新。

2. 衡量知识冲突

2.1 Preliminaries

​ 数据集$X=[(c_1,q_1,y_1),\dots ,(c_N,q_N,y_N)]$包含N个元组实例，其中$c$是包含答案的上下文，$q$是一个问题，$y$是ground-truth答案。对于第$i$个实例，语言模型$f$输出一个答案$a_i=[a_i^1,\dots ,a_i^h,\dots ,a_i^H]$，其包含H个tokens。输入$x_i$包含通用的prompt P和问题$q_i$，即$x_i=[P;q_i]$；或者还包含上下文$c_i$，即$x_i=[P;c_i,q_i]$。

2.2 语义不确定性分数(Semantic Uncertainty Score)

​ 使用语义不确定性分数来衡量intra-memory冲突。

​ 给定输入$x_i$，其包含通用prompt和问题$q_i$，先生成K个答案$A=[a_{i,0},a_{i,1},\dots ,a_{i,K}]$。然后，根据语义相似度对答案进行分组。使用DeBERTA NLI模型计算两个答案的语义相似度。根据语义相似度分组后会得到V个分组$G=[g_1,g_2,\dots ,g_V]$。

​ 通过语言集合之间的熵来衡量语言不确定性。首先，获得$p(g_v|q_i)$，模型生成答案$g_v$的概率
$$\begin{gathered} p(g_v|x_i)=\sum _{a_{i,k}\in g_v}p(a_{i,k}|x_i)=\sum _{a_{i,k}\in g_v}\prod _{h}p(a_i^h|a_i^{<h},x_i) \\ \text{\hspace{1em}(1)} \end{gathered}$$
有了分组概率后，使用蒙特卡洛积分来近似$x_i$语义熵的期望
$$\begin{gathered} \text{SE}(x_i)\approx -V^{-1}\sum _{v=1}^V\log p(g_v|x_i) \\ \text{\hspace{1em}(2)} \end{gathered}$$

2.3 连贯说服分数(Coherent Persuasion Score)

​ 使用连贯说服分数衡量context-memory冲突。在先前的工作中，说服分数用于观察上下文多大程度改变LM的答案。然而，现有的说服分数侧重在单个生成答案的第一个token，被认为不足以代表整体生成的序列。为了克服弊端，提出了连贯说服分数(Coherent Persuasion, CP)。

​ 为了计算$c_i$的CP分数，收集两组答案$A_{q_i}$和$A_{c_i\&q_i}$，其对应两组不同的输入$[P;q_i]$和$[P;c_i;q_i]$。然而，创建分组$G_{q_i}=[g_1,g_2,\dots ,g_r,\dots ,g_R]$和$G_{c_i\&q_i}=[g_1,g_2,\dots ,g_u,\dots ,g_U]$。CP分数通过平均$G_{c_i\&q_i}$和$G_{q_i}$的概率分布来获得。具体来说，$g_r$的概率分布表示为$p_{g_r}$：
$$\begin{gathered} p_{g_r}=\frac{1}{W}\sum _{w=1}^W{p}_{a_w} \\ \text{\hspace{1em}(3)} \end{gathered}$$
其中$g_v$有W个生成答案且$p_{a_w}$是答案$a_w$中所有token的概率分布的平均值。最终的CP分数为
$$\begin{gathered} CP(c_i)=\frac{1}{|R|\times |U|}\sum _{r=1}^R\sum _{u=1}^{U}k{l}_{div}(p_{g_r},p_{g_i}) \\ \text{\hspace{1em}(4)} \end{gathered}$$
因为CP分数衡量$A_{q_i}$和$A_{c_i\&q_i}$的概率分布距离，其表明LM概率分布受上下文影响的程度。

3. DYNAMICQA$

$$\begin{gathered} (c_i)=\frac{1}{|R|\times |U|}\sum _{r=1}^R\sum _{u=1}^{U}k{l}_{div}(p_{g_r},p_{g_i}) \\ \text{\hspace{1em}(4)} \end{gathered}$$
因为CP分数衡量$A_{q_i}$和$A_{c_i\&q_i}$的概率分布距离，其表明LM概率分布受上下文影响的程度。

3. DYNAMICQA

​ 为了评估上述方法，构造了一个包含11378问答对的数据集。