深入剖析Self-Attention自注意力机制【图解】
文章目录
- 1、简介
- 2、Sequence Labeling
- 3、Self-attention计算过程
- 3.1、总览
- 3.2、attention scores
- 3.3、Softmax
- 3.4、value(V)
- 3.5、Output
- 4、矩阵(向量)角度
- 5、Self-attention的其他应用
- 5.1、音频处理
- 5.2、图像处理
- 6、Self-attention v.s.CNN
- 7、Self-attention v.s.RNN
🍃作者介绍:双非本科大四网络工程专业在读,阿里云专家博主,专注于Java领域学习,擅长web应用开发、数据结构和算法,初步涉猎人工智能和前端开发。
🦅个人主页:@逐梦苍穹
📕所属专栏:人工智能
🌻gitee地址:xzl的人工智能代码仓库
✈ 您的一键三连,是我创作的最大动力🌹
1、简介
下一章是关于Self-Attention的代码实现:https://xzl-tech.blog.csdn.net/article/details/141330440
Self-Attention是一种在深度学习中用于建模序列数据(如文本、图像、语音等)内部依赖关系的机制;
它最初在Transformer模型中引入,并迅速成为许多自然语言处理和计算机视觉任务的核心组件。
Self-Attention的基本思想是,通过计算序列中每个元素与其他所有元素之间的相关性(即注意力得分),动态调整模型对不同部分的关注度;
这一机制使得模型能够灵活地捕捉长程依赖关系,而不需要像循环神经网络(RNN)那样顺序处理输入序列
2、Sequence Labeling
Sequence Labeling(序列标注)是一类非常重要的自然语言处理(NLP)任务,涉及对输入序列中的每个元素进行标注或分类。常见的应用场景包括词性标注(POS tagging)、命名实体识别(NER)、分词、拼写纠正以及语音识别中的音素标注等
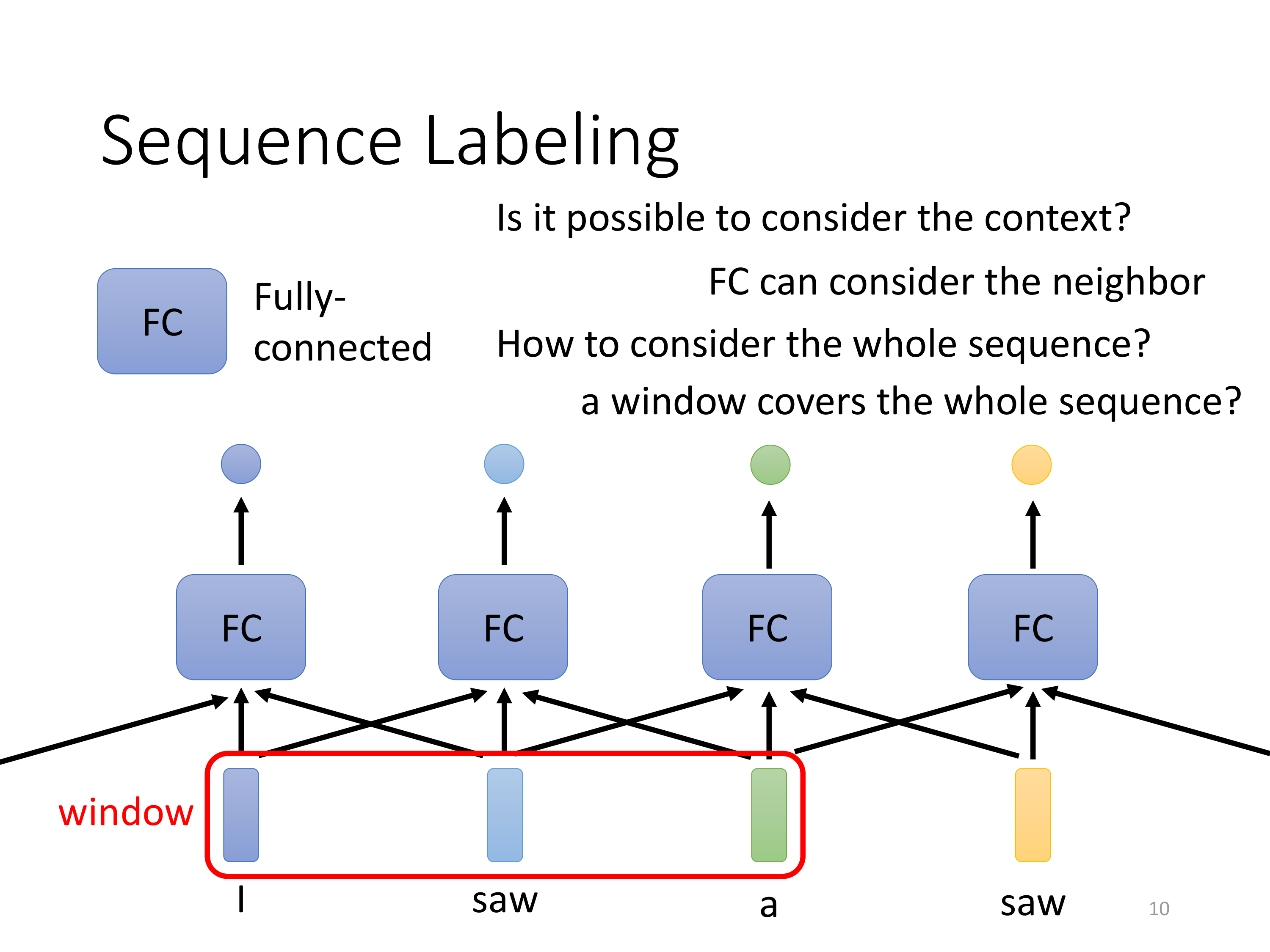
关于上面这张图:
- 展示了在序列标注(Sequence Labeling)任务中,如何使用全连接层(Fully-Connected, FC)来处理上下文信息,以及它的局限性;
- 这张图的意义在于展示了传统全连接层在处理序列标注任务时的局限性,即难以捕捉全局上下文信息,这也为后续引入更复杂的机制(如Self-Attention)铺垫了背景。
Self-Attention可以在不依赖于固定窗口的情况下,灵活地处理序列中的长程依赖关系,使得模型更具表达力和泛化能力。

如上图引入一个滑动窗口,模型可以同时关注输入序列中的多个元素;
这种方式能够考虑一定范围内的上下文,但仍然存在局限性,因为它只能覆盖一个固定的局部区域
局部上下文 vs. 全局上下文:全连接层虽然可以通过滑动窗口的方式捕捉局部上下文,但在处理长序列或需要全局信息的任务中,效果有限。要考虑整个序列的上下文信息,通常需要引入像RNN或Self-Attention这样的机制。
Self-Attention的引入:相比于全连接层,Self-Attention机制能够动态计算输入序列中每个元素之间的相关性,从而在生成输出时同时考虑整个序列的上下文信息。这种机制不受固定窗口的限制,能够更好地捕捉远距离依赖。
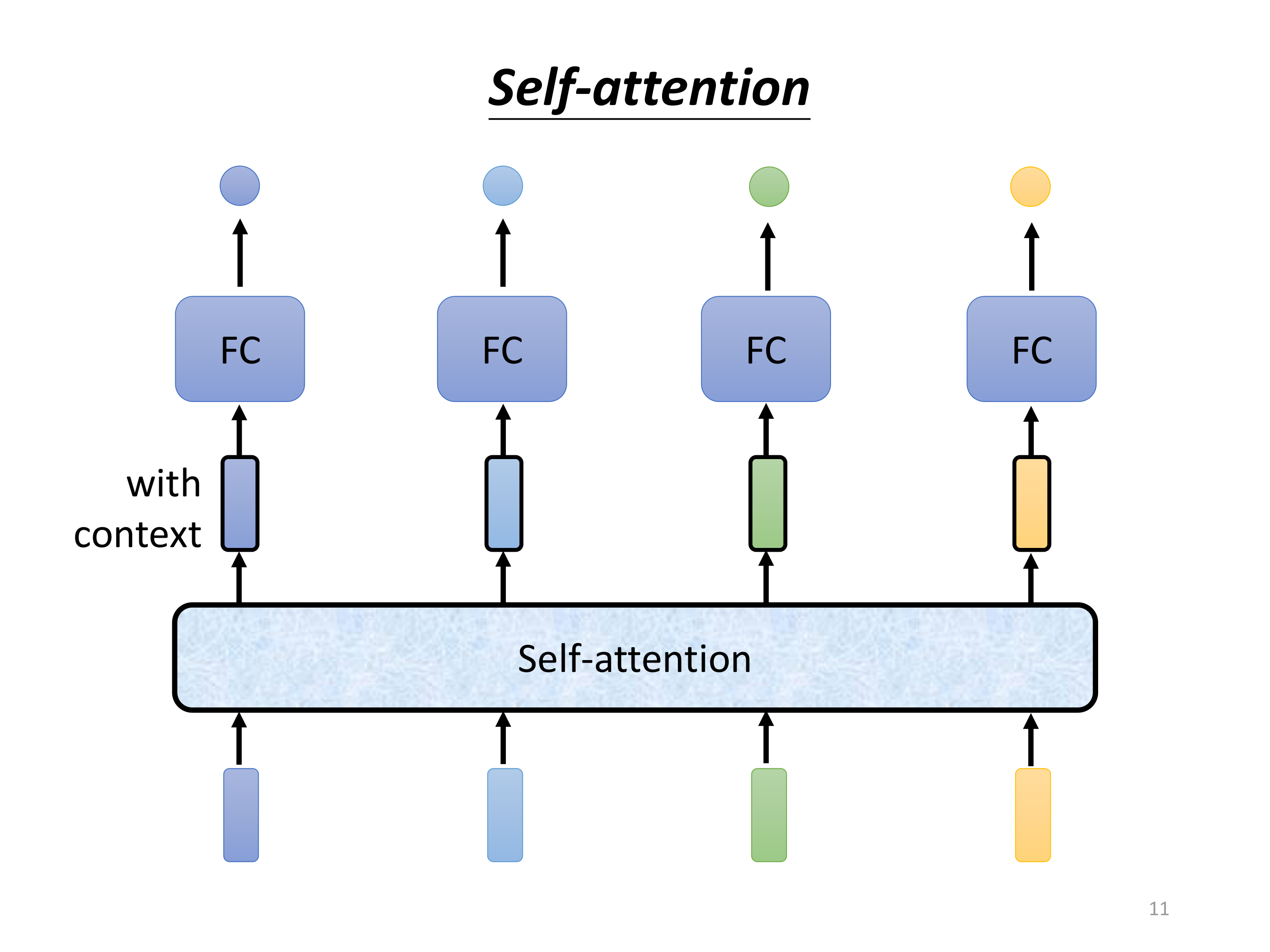
下面进入本章的主角:Self-attention
3、Self-attention计算过程
3.1、总览
如图所示:
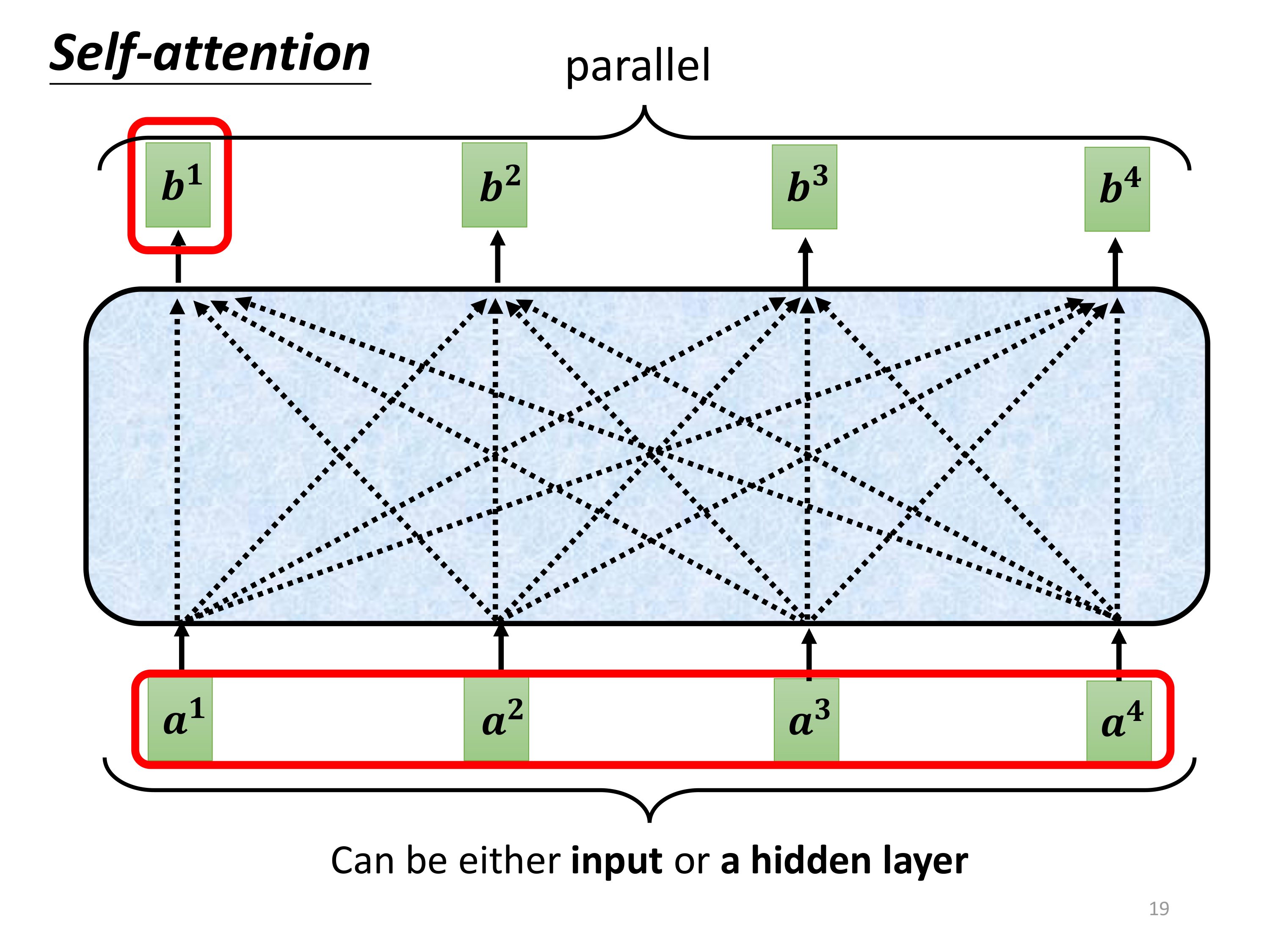
a i a^i ai表示输入,可以是输入也可以是某个隐藏层的输出;
b i b^i bi表示经过了Self-attention的输出。
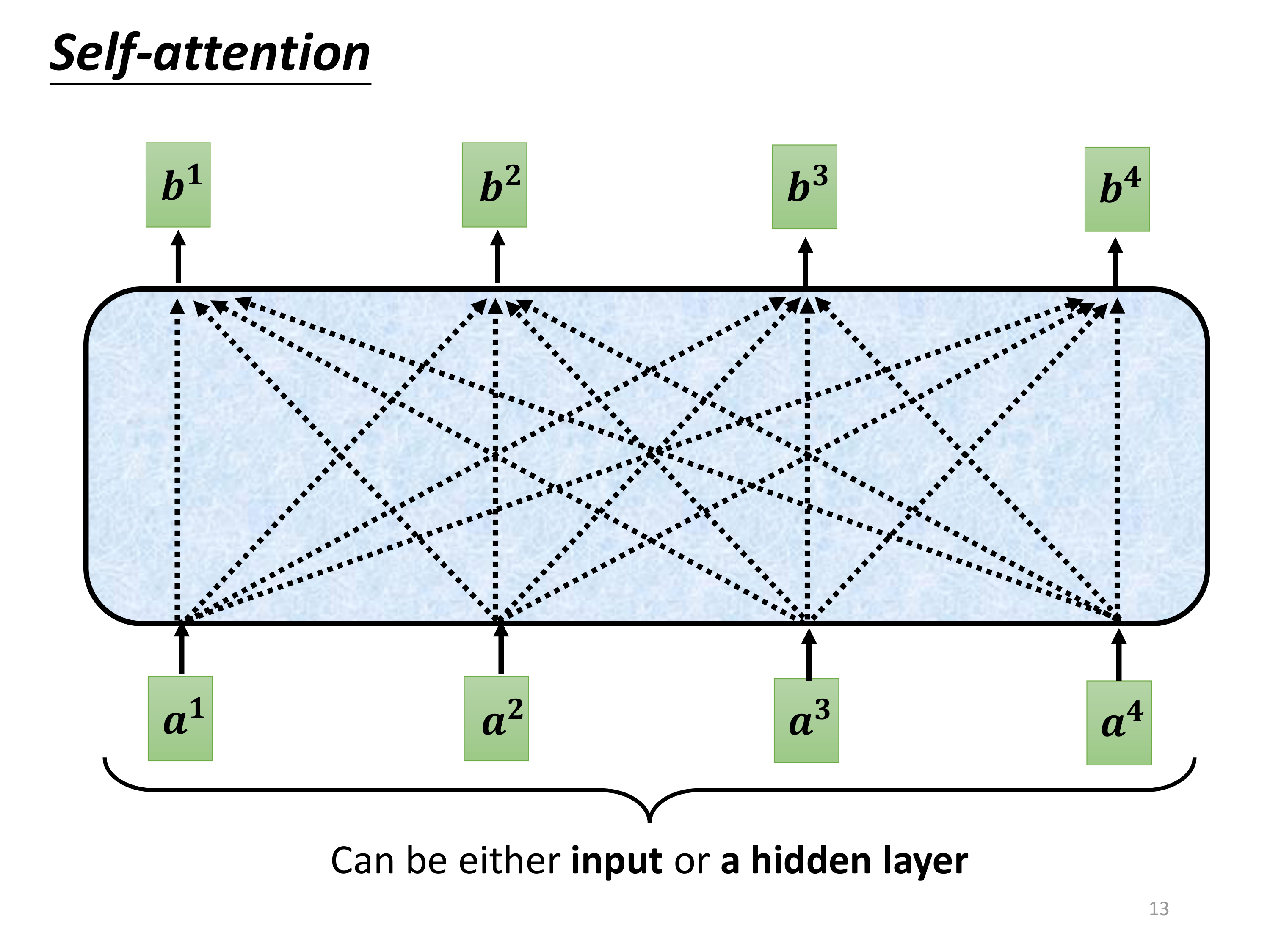
那么整个 Self-attention, 其实就是一个从 a i a^i ai到 b i b^i bi的过程;
从 a i a^i ai到 b i b^i bi,需要经历一个计算 α \alpha α的值,这个就是所谓的attention scores
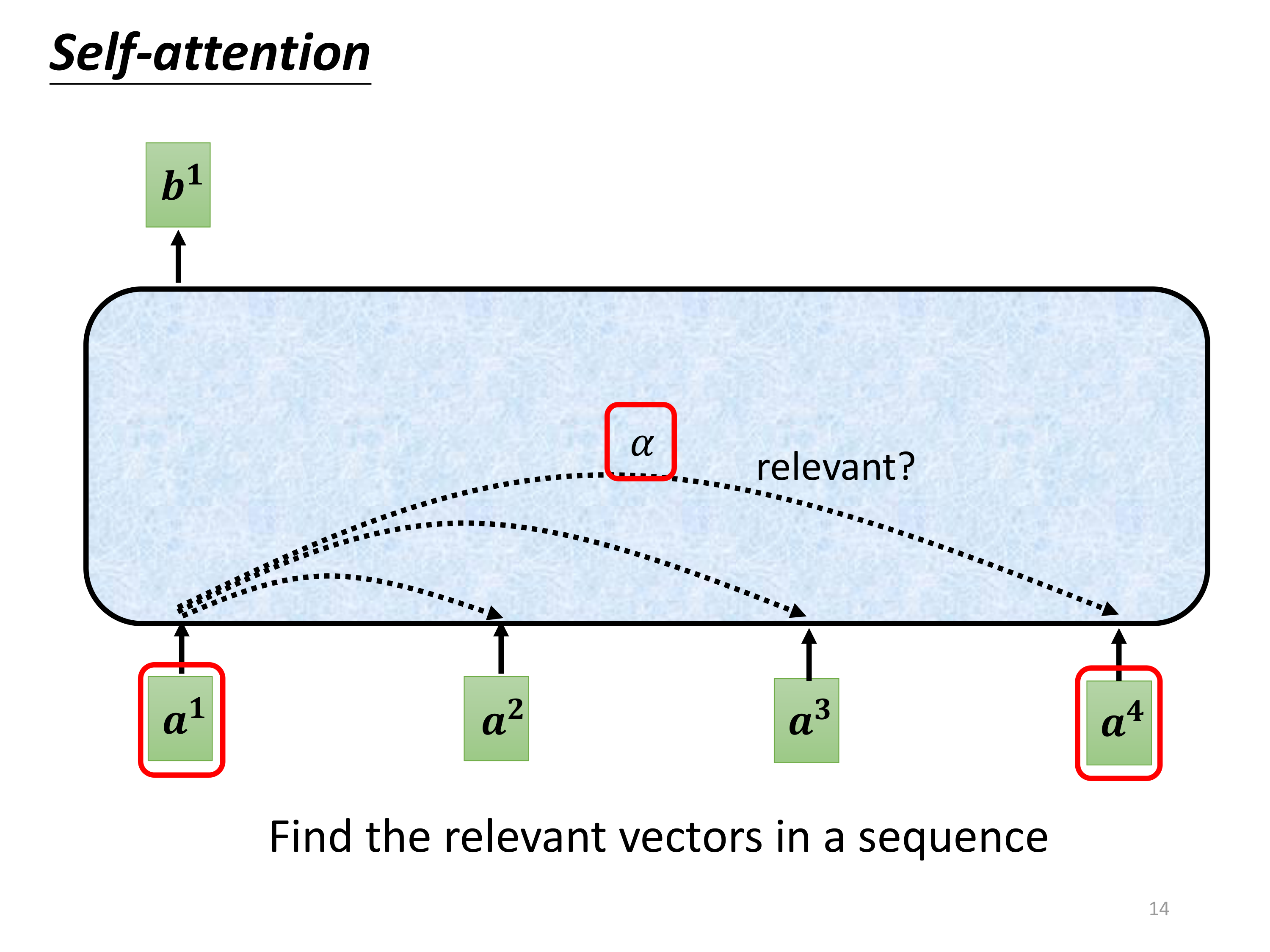
3.2、attention scores
关于这个 α \alpha α如何计算,下图展示了两种方式(Dot-product和Additive):
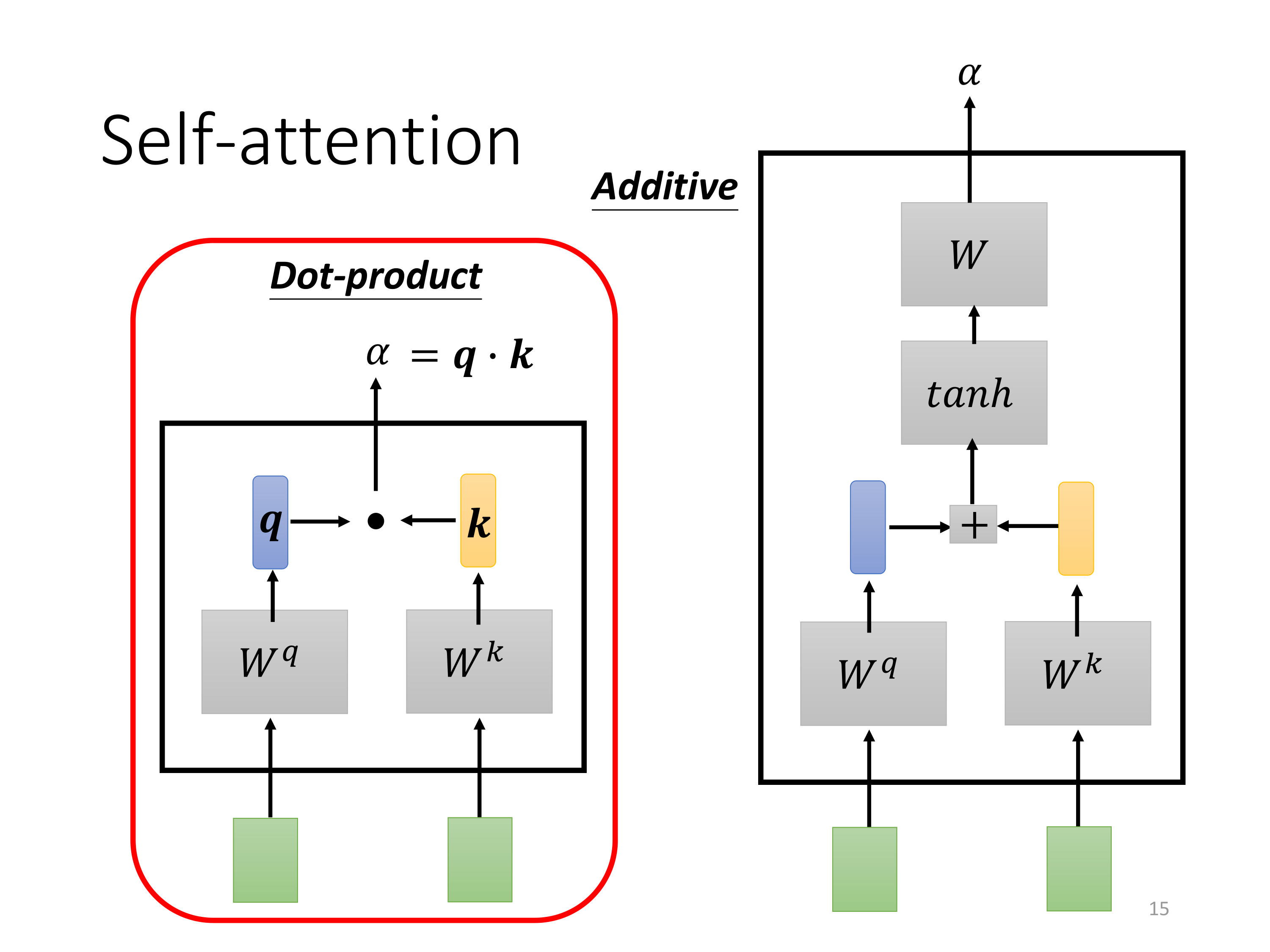
- 点积注意力(Dot-product Attention): Attention ( Q , K , V ) = Softmax ( Q ⋅ K T d k ) ⋅ V \text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{Q \cdot K^T}{\sqrt{d_k}}\right) \cdot V Attention(Q,K,V)=Softmax(dkQ⋅KT)⋅V
图中的左侧框架展示了点积注意力的计算:查询向量 q q q与键向量 k k k通过点积运算生成注意力得分 α \alpha α
这个方法计算简单高效,适用于大多数实际应用,尤其是 Transformer 模型中。
- 加性注意力(Additive Attention): Attention ( Q , K , V ) = Softmax ( sum ( tanh ( Linear ( [ Q , K ] ) ) ) ) ⋅ V \text{Attention}(Q, K, V) = \text{Softmax}(\text{sum}(\tanh(\text{Linear}([Q, K])))) \cdot V Attention(Q,K,V)=Softmax(sum(tanh(Linear([Q,K]))))⋅V
右侧框架展示了加性注意力的计算过程。这里 q q q和 k k k的组合会先通过一个全连接层,再通过 t a n h tanh tanh激活函数进行处理,最后通过另一个全连接层生成注意力得分 α \alpha α。
虽然计算复杂度稍高,但加性注意力在低维度的场景下往往表现更好,特别是在需要 更强非线性表达能力的任务中。
本文就围绕Dot-product来进行讲解。
还记得我在上文提到“从 a i a^i ai到 b i b^i bi,需要经历一个计算 α \alpha α的值”,此 α \alpha α非彼 α \alpha α。
经过Dot-product处理的是“局部的 α \alpha α”实际上应该说是 α i j \alpha_{ij} αij,而最终需要的是一个考虑全局上下文信息的 α \alpha α,
请继续往下看(这里拿 a 1 a^1 a1进行举例):
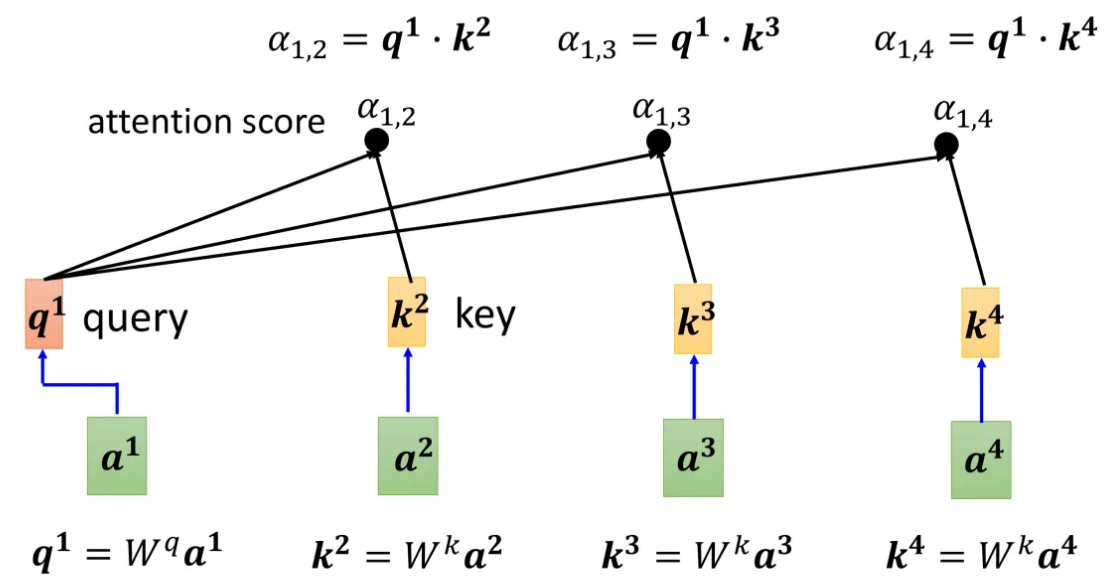
上图的计算流程:
- 查询(Query):由输入 a 1 a^1 a1生成的查询向量 q 1 q^1 q1,是用来查询与其相关的键向量的。
- 键(Key):每个输入向量通过线性变换生成的键向量(如 k 2 k^2 k2, k 3 k^3 k3, k 4 k^4 k4),用于计算与查询向量的相似度。
- 点积计算:查询向量与每个键向量进行点积,计算出注意力得分 α \alpha α,这些得分反映了序列中各元素对生成当前输出的重要性
3.3、Softmax
生成了 α 1 , i \alpha_{1,i} α1,i之后,经过 S o f t m a x Softmax Softmax函数归一化处理,得到 α 1 , i ′ \alpha'_{1,i} α1,i′:
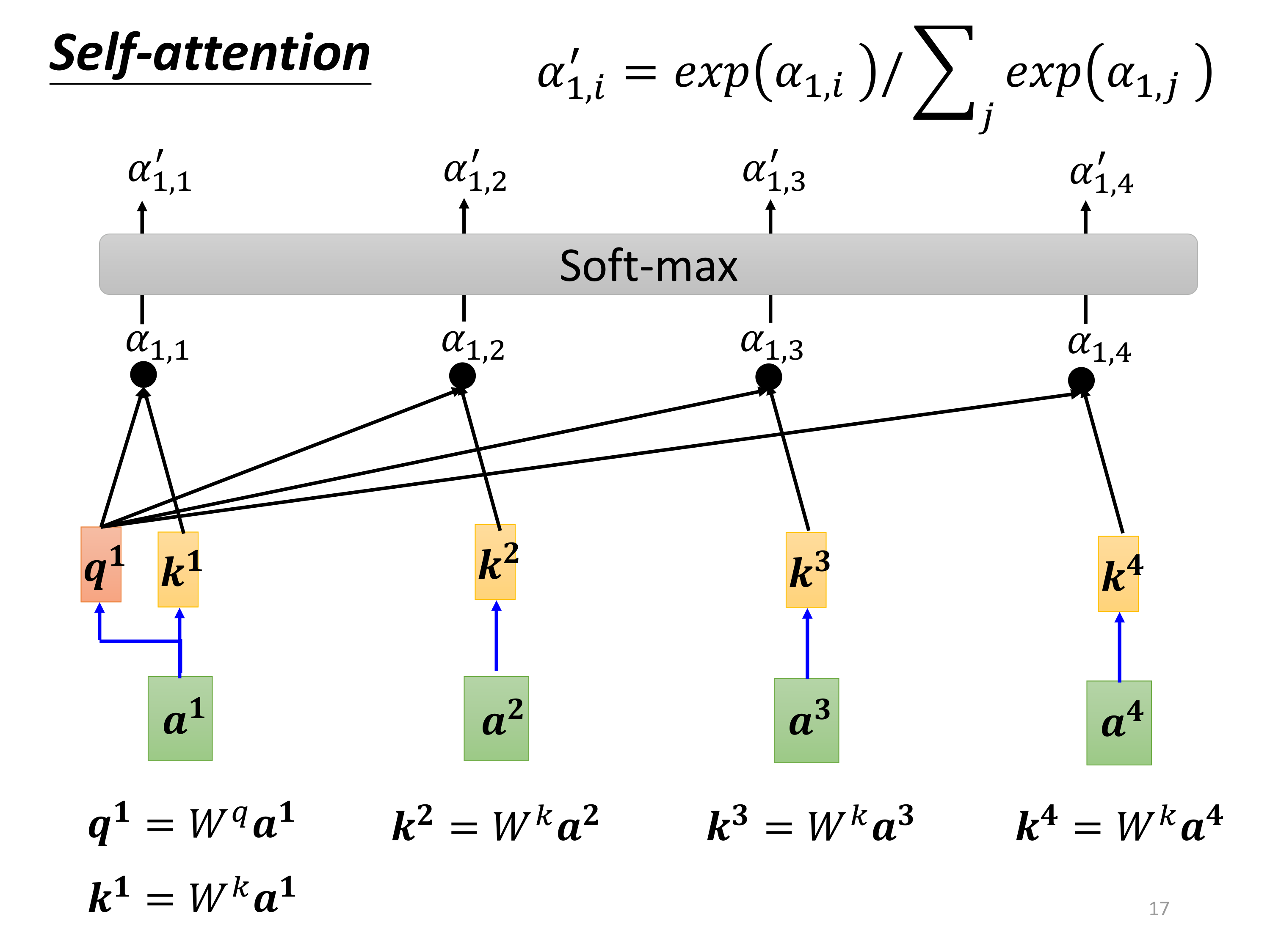
Softmax归一化的必要性:
- S o f t m a x Softmax Softmax函数的引入不仅是为了确保权重的可解释性(作为概率分布),还解决了在点积计算中可能出现的数值不稳定问题
- 特别是在点积结果范围较大时, S o f t m a x Softmax Softmax能够有效控制权重的数值范围。
3.4、value(V)
现在是需要计算value的值,我们把 a 1 a^1 a1到 a 4 a^4 a4的每一个向量vector,乘上 W v W^v Wv得到新的vector:
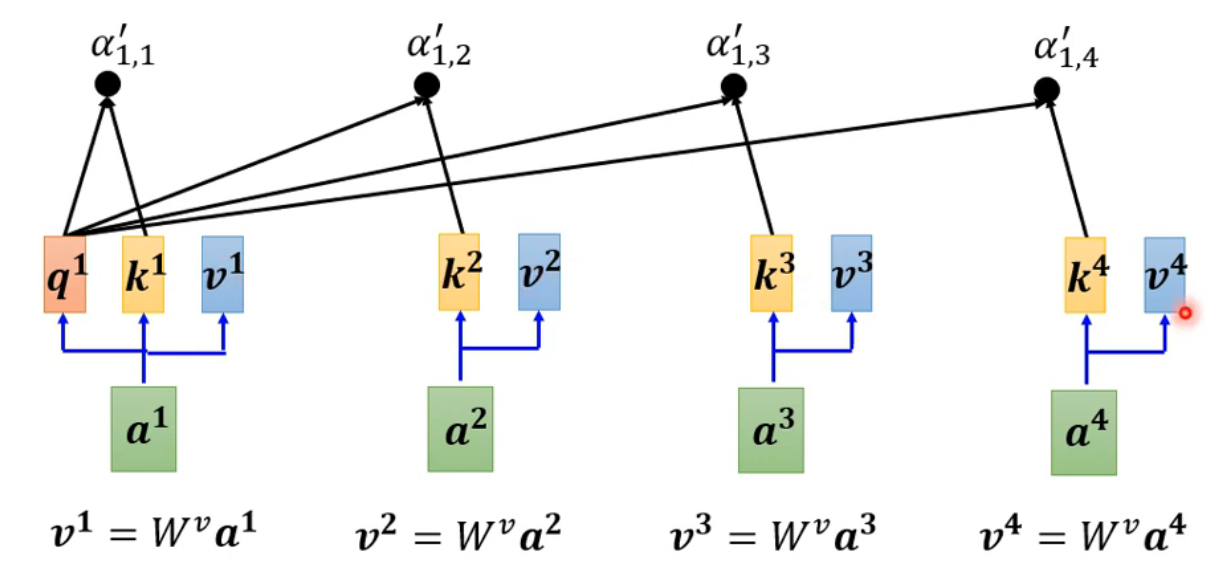
3.5、Output
再往下是根据attention scores来提取信息(information),这里就是上面提到的由 a i a^i ai生成 b i b^i bi:
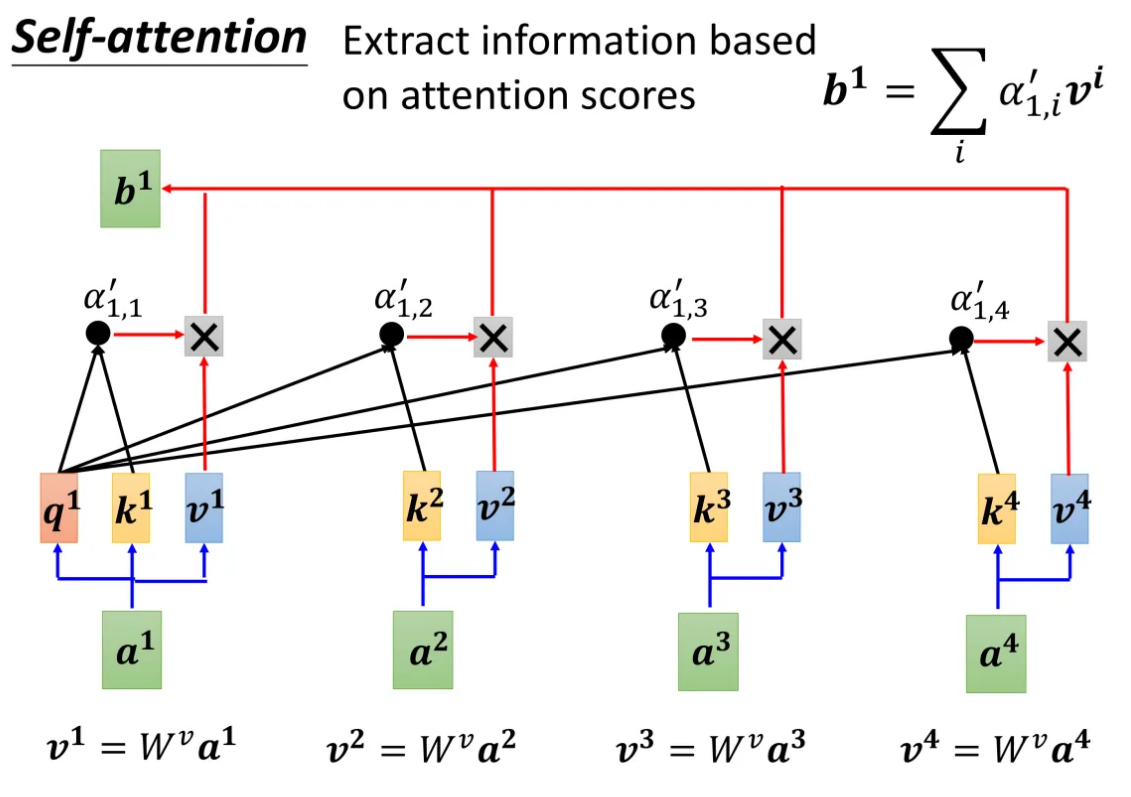
每一个经过 S o f t m a x Softmax Softmax函数归一化处理后的attention scores α 1 , i ′ \alpha'_{1,i} α1,i′,乘上对应的 v i v^i vi,就是得到最终的 b i b^i bi
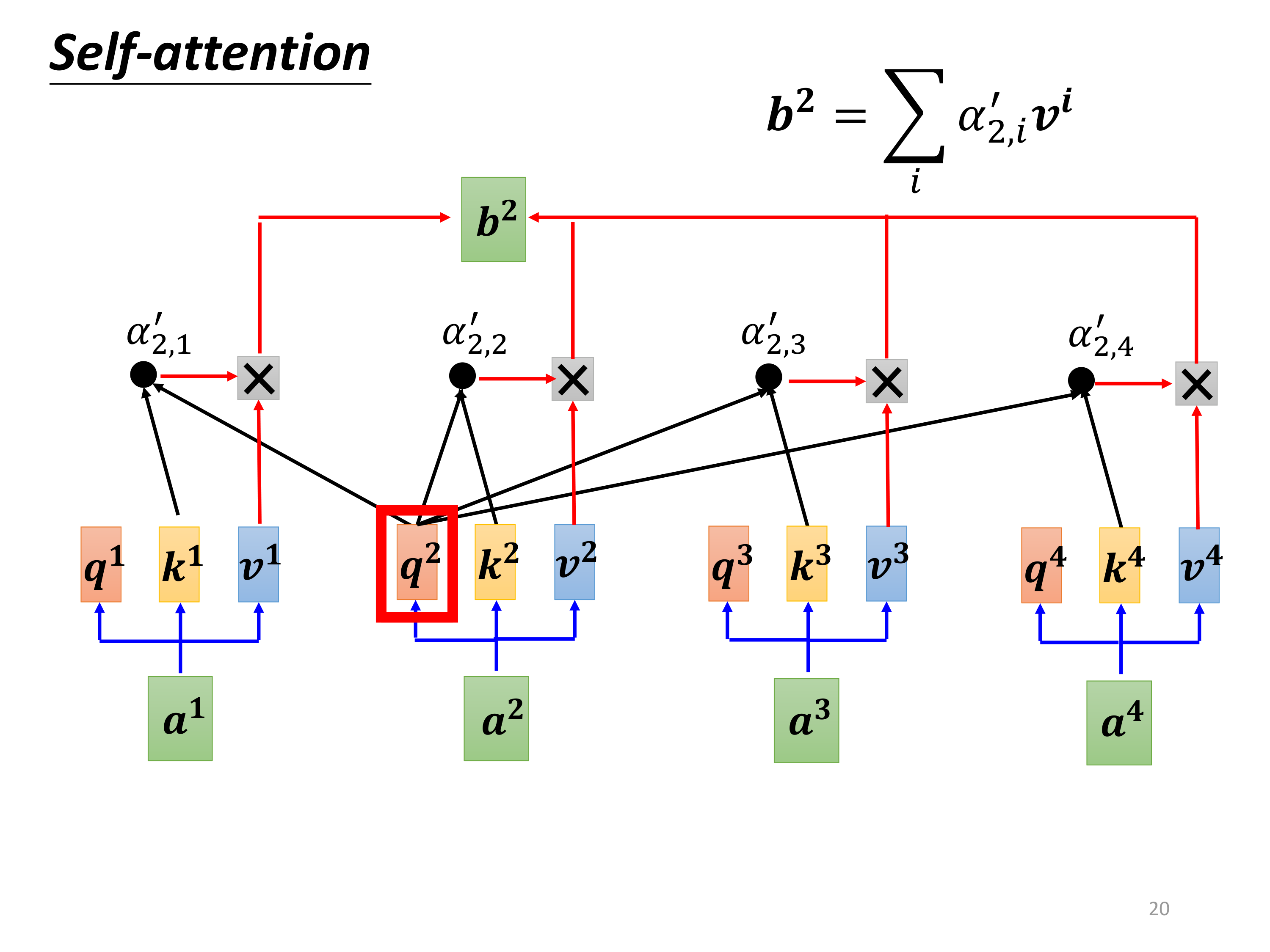
对 b 2 b^2 b2的计算同理:
4、矩阵(向量)角度
经过上面的处理,我们发现,其实可以看成是各个矩阵(或向量)的运算。
把 a 1 a^1 a1到 a 4 a^4 a4看成是一个矩阵 I I I,矩阵 I I I乘以矩阵 W q W^q Wq得到矩阵 Q Q Q、乘以矩阵 W k W^k Wk得到矩阵 K K K、乘以矩阵 W v W^v Wv得到矩阵 V V V:
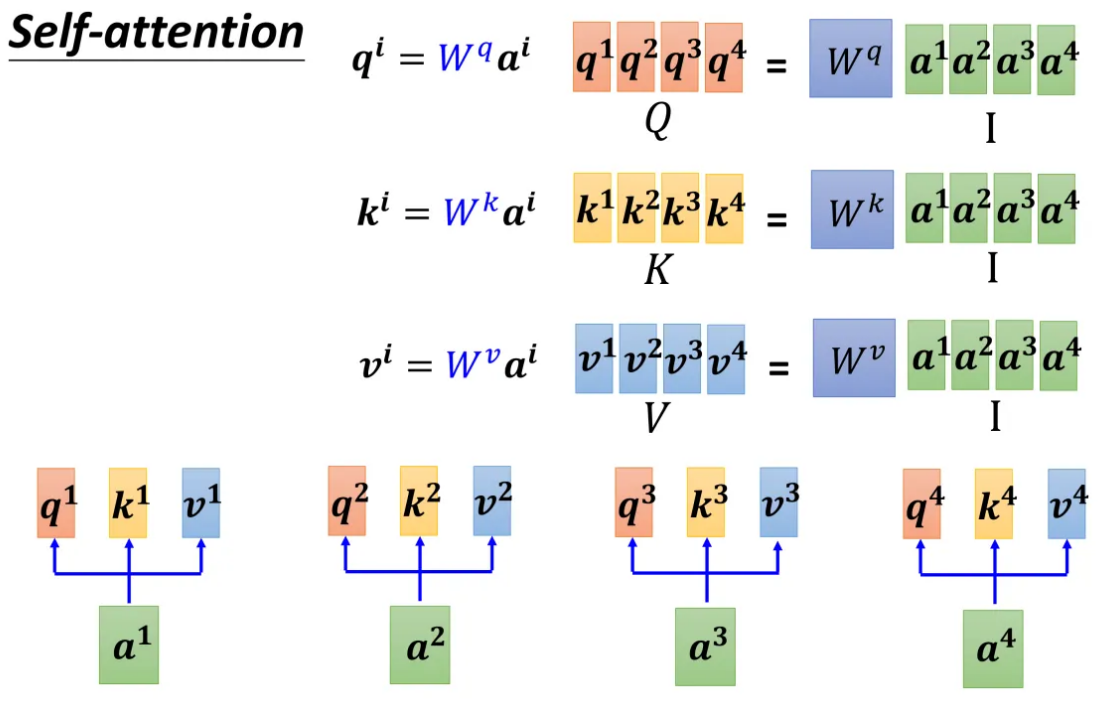
对于 α \alpha α的计算同样如此:矩阵 k i [ i = 1 , 2 , 3 , 4 ] k^i[i=1,2,3,4] ki[i=1,2,3,4]乘以 q 1 q^1 q1,得到矩阵 α 1 , i [ i = 1 , 2 , 3 , 4 ] \alpha_{1,i}[i=1,2,3,4] α1,i[i=1,2,3,4]:
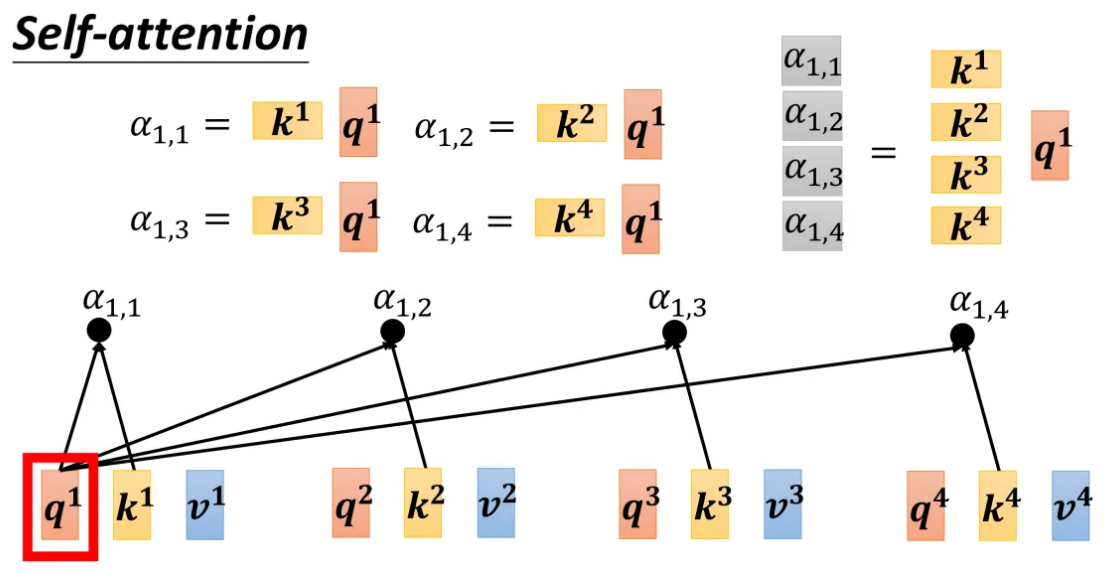
对于 α i , j \alpha_{i,j} αi,j(这里用 A A A表示)经过 S o f t m a x Softmax Softmax函数得到 α i , j ′ \alpha'_{i,j} αi,j′(这里用 A ′ A' A′表示):

最后由矩阵 A ′ A' A′乘以矩阵 V V V得到最终由 b i b^i bi组成的矩阵 O O O,也就是最终的Output:
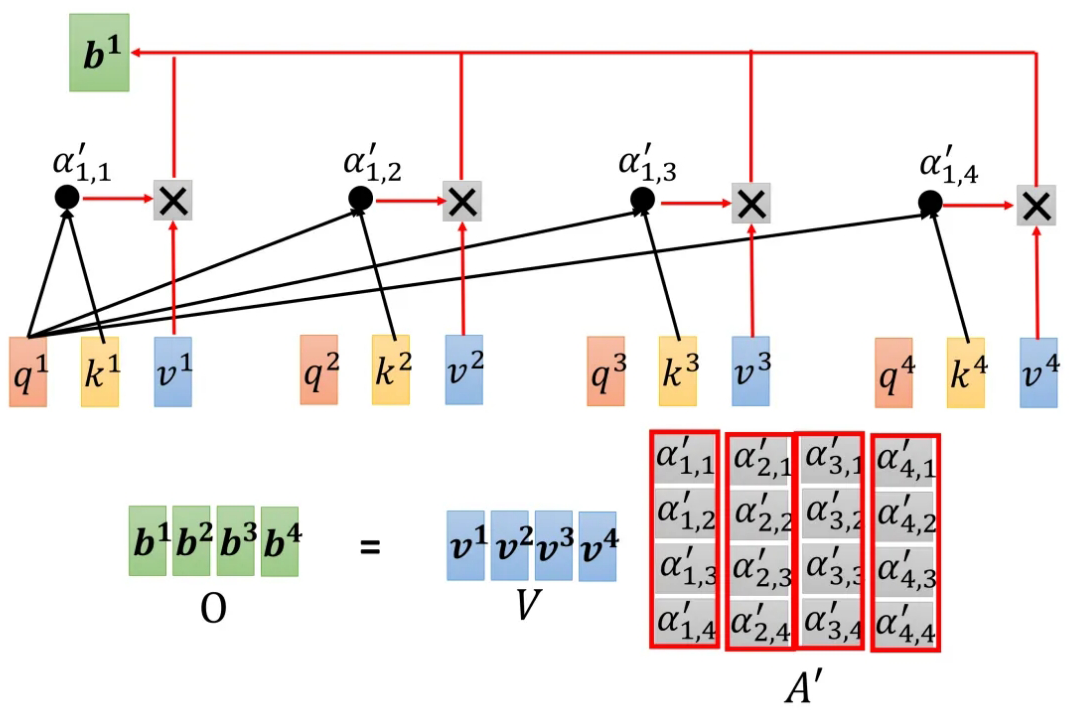
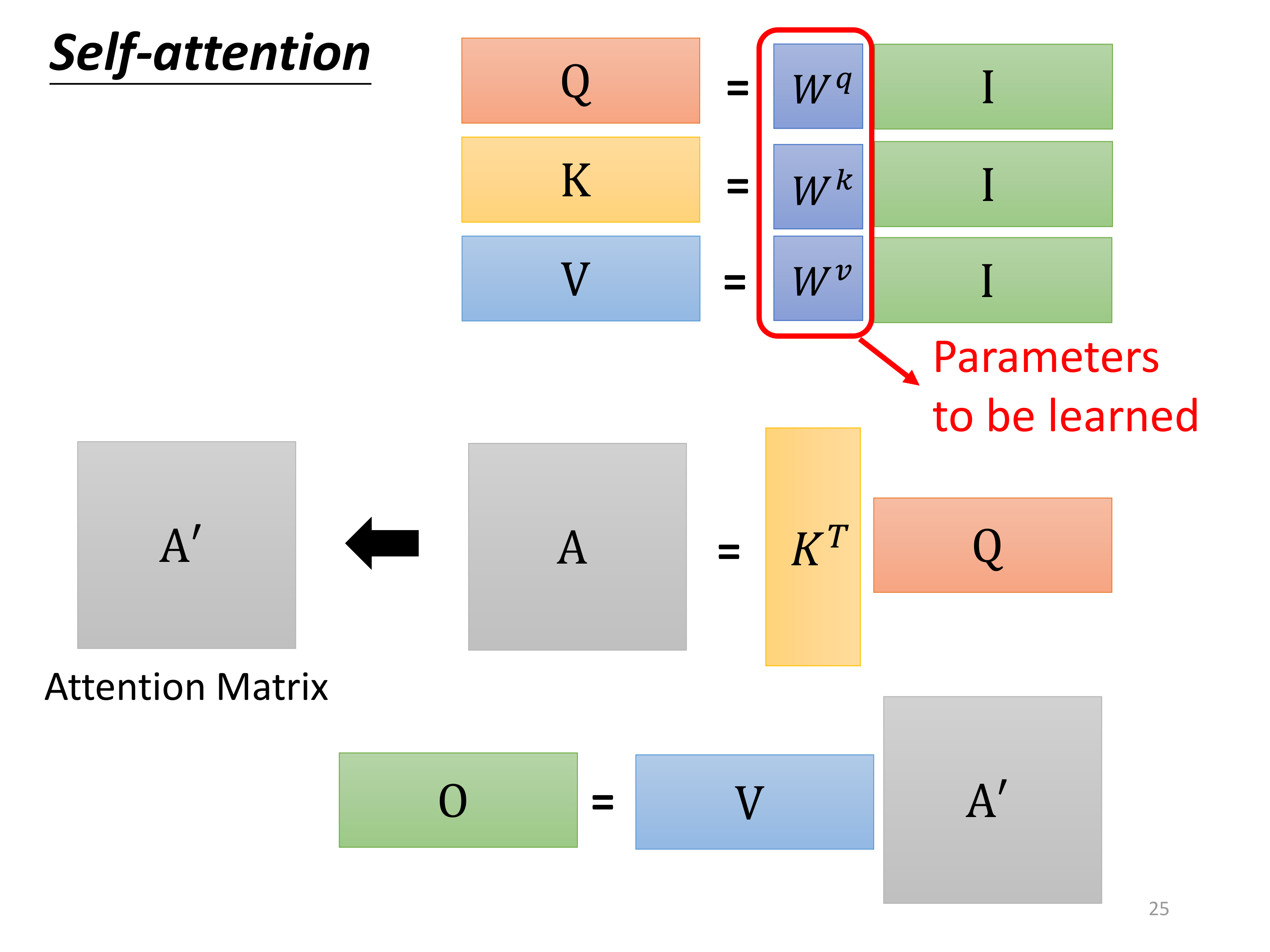
所以,回顾整个Self-attention的计算过程,可以发现只有 W q W^q Wq、 W k W^k Wk、 W v W^v Wv三个矩阵是需要学习的未知参数:
5、Self-attention的其他应用
5.1、音频处理
在对音频处理上,这里还有一个Truncated Self-attention。
这张图展示了Self-Attention在语音处理中的应用,特别是针对长序列数据的截断注意力(Truncated Self-Attention);
语音信号通常是非常长的向量序列,因此处理时需要特别的优化策略。
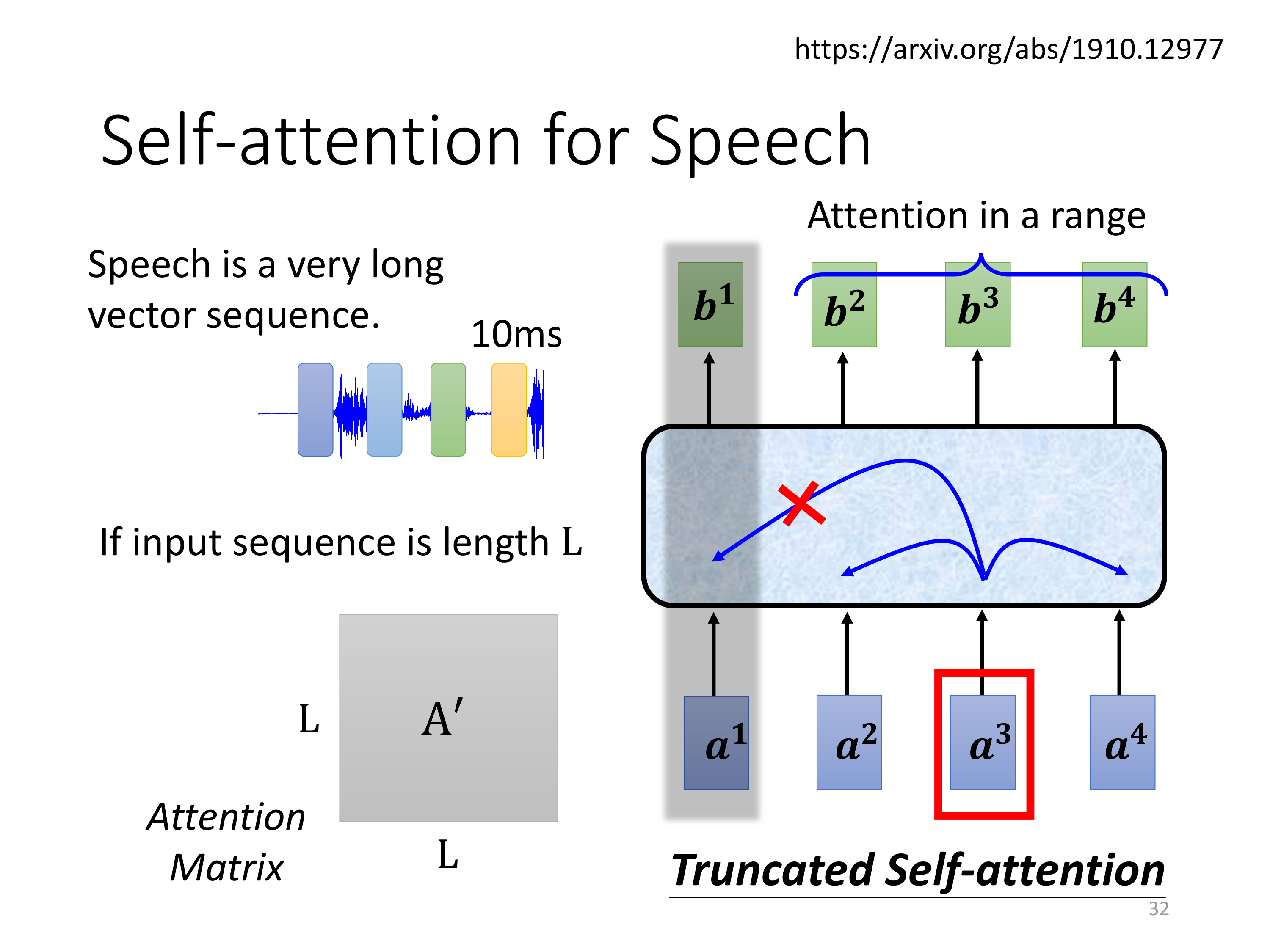
语音序列的特性:
- 语音是一个非常长的向量序列,通常每10毫秒就会生成一个数据点,随着时间的推移,语音数据会形成一个长度很长的序列;
- 如果直接对整个长序列应用标准的Self-Attention机制,计算的复杂度会非常高
截断注意力(Truncated Self-Attention)的引入:
- 为了降低计算复杂度,截断注意力只在一定范围内计算注意力得分,即对某个输入向量,只与其相邻的部分向量进行相关性计算。
- 图中展示了 a 3 a^3 a3只关注其相邻的一些向量 a 2 a^2 a2和 a 4 a^4 a4,而不是整个序列。这种机制在长序列处理时可以显著减少计算量。
截断注意力的优势:
- 计算效率:通过限制注意力计算的范围,使得模型在处理长序列时更加高效;
- 局部上下文的关注:虽然截断注意力减少了计算量,但它仍能在一个合理的范围内捕捉到局部上下文信息,确保输出的准确性
在语音处理中的应用:
- 在语音处理中,语音信号的短时间变化通常具有局部相关性,因此截断注意力可以有效捕捉这些短时依赖关系
- 例如,在语音识别或说话人识别中,语音片段的相邻部分往往包含相关信息,因此截断注意力可以帮助模型更好地理解语音数据
5.2、图像处理
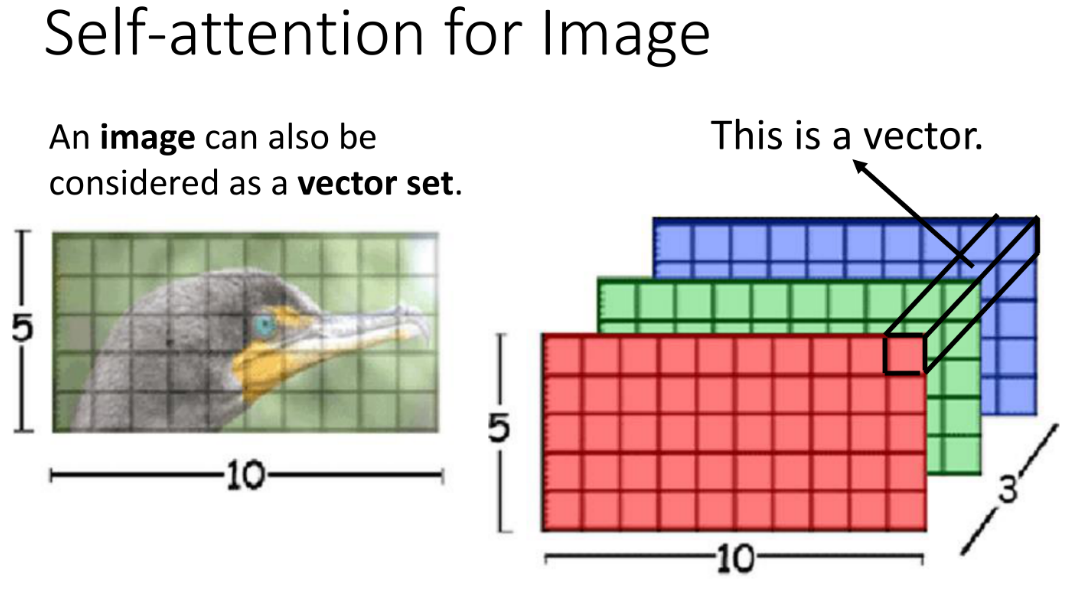
图像被视为一个向量集(vector set),其中每个向量表示图像中的一个像素或一个小区域;
图像通常由像素网格组成,每个像素具有多通道(如RGB三个通道)的数值表示。
- 图中的例子展示了一张5x10的图片,每个像素点的颜色由红、绿、蓝三个值组成,这些值可以被视为一个3维向量;
- 整张图像可以被表示为一个由这些3维向量组成的集合,即一个“向量集”;
- 每一个向量,就是当前像素点的“红绿蓝”
Self-Attention在图像中的应用
- 像素间的依赖关系:
Self-Attention可以用来捕捉图像中不同区域之间的相关性。
例如,一个像素(或区域)不仅可以受到其周围像素的影响,还可以与图像中其他更远的区域相关联。
在图中,右边的红、绿、蓝三层矩阵表示图像中对应的RGB通道,每个通道的值可以视为一个向量(如图中箭头所指的地方)
通过Self-Attention,这些向量可以互相“交流”,模型可以在全局范围内理解图像的内容
- Self-Attention的计算过程:
和处理文本序列类似,Self-Attention机制会为每个像素(或区域)的向量生成查询(Query)、键(Key)和值(Value),然后通过计算查询和键之间的相关性,决定每个像素对其他像素的注意力权重;
这些权重会用于加权其他像素的值向量,从而更新当前像素的表示;
这一机制允许模型灵活地聚焦于图像中的不同区域,根据上下文调整对不同像素的关注度
6、Self-attention v.s.CNN
CNN能做的很多事情,其实用Self-attention都能实现。
先说结论:Self-attention可以看成是加强版本的CNN。
具体不再展开了,请看下列图片:
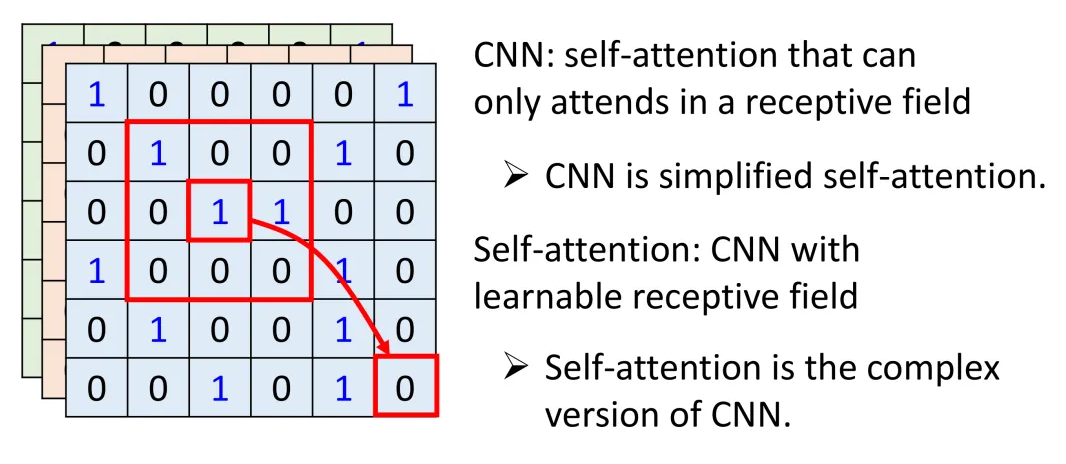
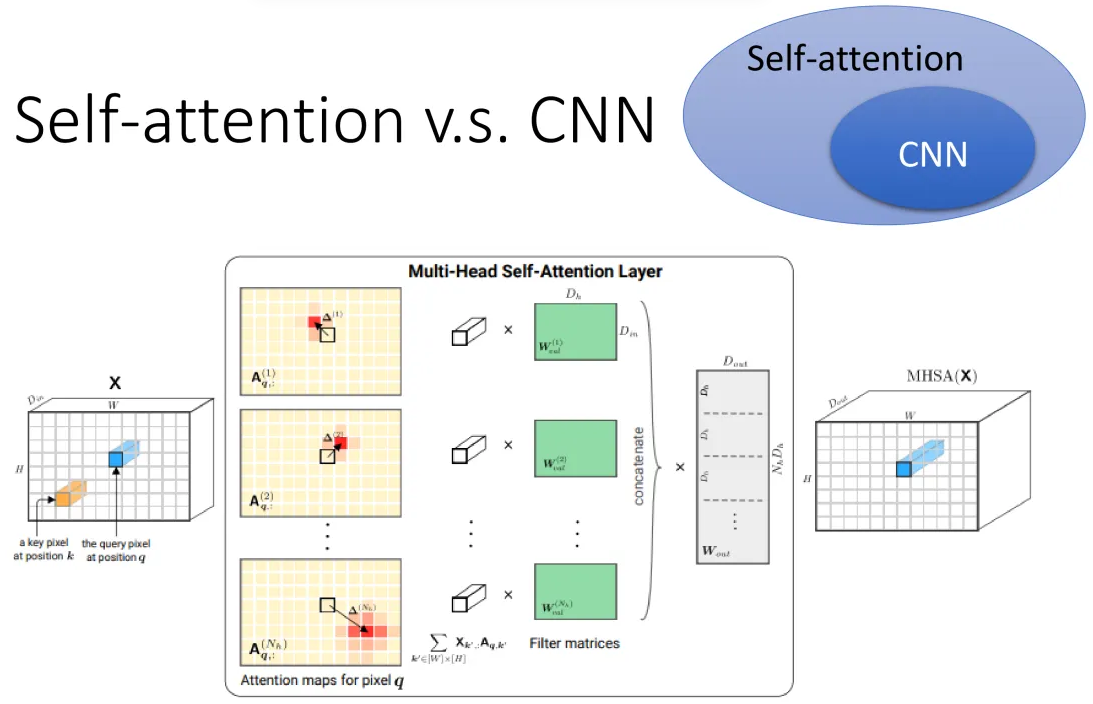
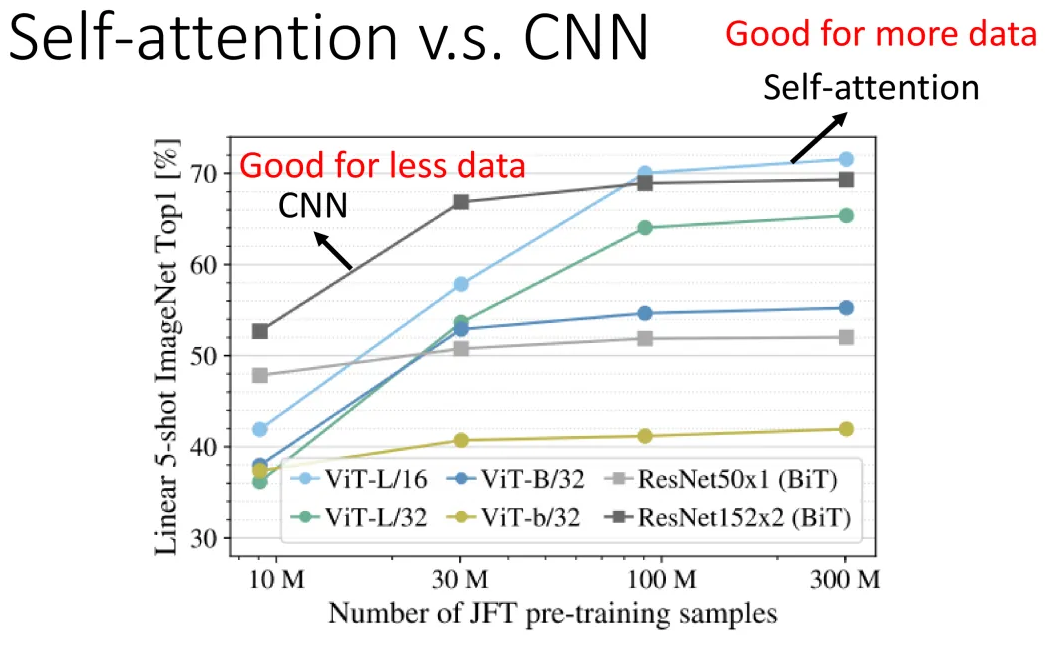
7、Self-attention v.s.RNN
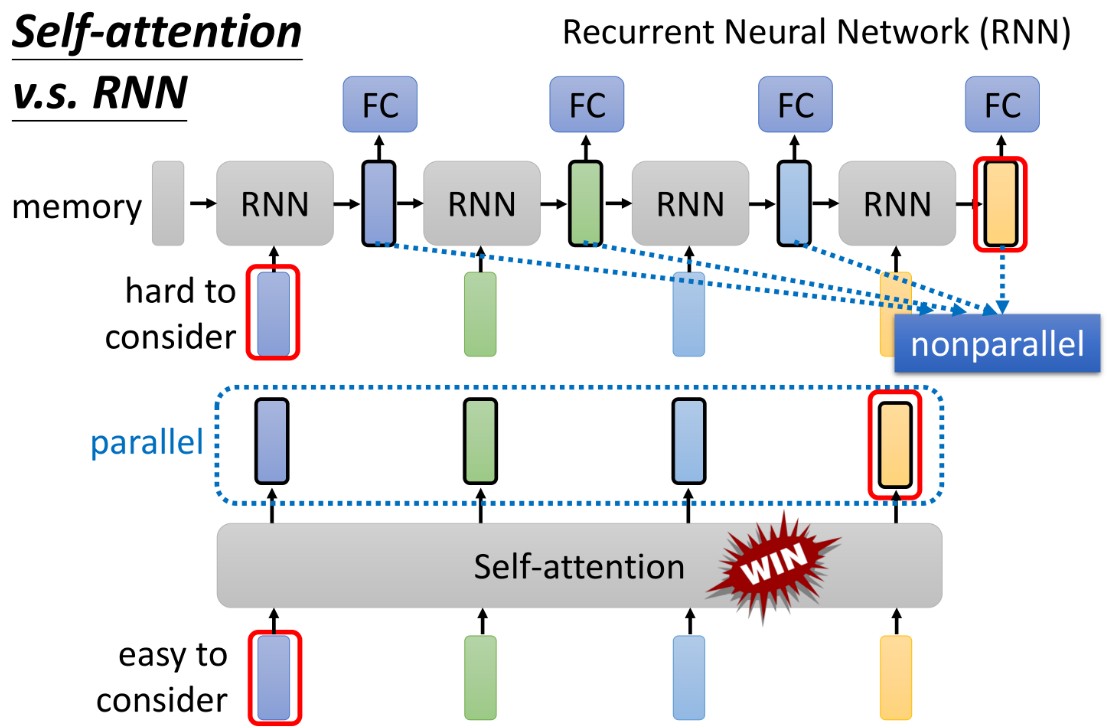
这张图对比了Self-Attention 和 循环神经网络(RNN) 在处理序列数据时的不同特点,展示了Self-Attention在并行处理和全局依赖关系建模方面的优势。
RNN的特点:
- 顺序处理(Sequential Processing):
- RNN处理序列数据时,依赖于序列的顺序,即每个时间步的输出依赖于前一个时间步的状态。这意味着RNN是非并行的(nonparallel),因为每个时间步都必须等待前一个时间步的结果。
- 长程依赖问题(Long-term Dependencies):
- 当RNN处理长序列时,前面的状态信息需要通过多个时间步传递到后面的时间步。由于每个时间步只能依赖于前一个时间步的信息,这使得捕捉远距离的依赖关系变得困难。图中的“hard to consider”标记显示了RNN在处理长距离依赖时的局限性。
- 全连接层(Fully Connected, FC):
- 图中展示了RNN后接全连接层的结构,这通常用于生成输出。每个RNN单元传递信息到下一个RNN单元,并最终通过全连接层进行输出计算。
Self-Attention的特点:
- 并行处理(Parallel Processing):
- Self-Attention允许在处理序列时,所有元素可以同时被处理,因为每个元素与序列中的所有其他元素都直接进行交互。这意味着Self-Attention是并行的(parallel),可以更高效地利用计算资源。
- 全局依赖建模(Global Dependencies):
- Self-Attention机制通过计算序列中每个元素与所有其他元素的相关性,能够直接捕捉长程依赖关系。这种机制不依赖于顺序处理,因此可以轻松处理远距离的依赖。图中“easy to consider”标记展示了Self-Attention在处理长程依赖时的优势。
- 对比优势:
- 图中的“WIN”标记表明,Self-Attention在并行性和处理全局信息方面优于RNN,特别是在处理长序列数据时,Self-Attention能够更有效地捕捉到全局上下文。
应用场景与总结:
- RNN的应用:
- 尽管RNN在处理顺序性很强的任务(如时间序列预测、语音识别等)中仍有一定优势,但其处理长程依赖和并行计算的能力较弱,这在处理非常长的序列或需要全局信息的任务中会成为瓶颈。
- Self-Attention的应用:
- Self-Attention广泛应用于Transformer模型,特别是在自然语言处理(如翻译、摘要生成)和计算机视觉任务中。其并行处理能力和对全局信息的敏感性,使得Self-Attention成为处理复杂序列数据的优选方法。
最后总结:
- 这张图清楚地对比了RNN和Self-Attention在处理序列数据时的不同优势和局限
- Self-Attention由于其并行处理和全局依赖建模的能力,在许多应用中都胜过RNN,尤其是在需要高效处理长序列和复杂依赖关系的任务中
