【路径规划】基于人工势场(APF)算法、Vortex APF算法、Safe APF算法和动态 Windows 方法的比较

摘要
本文对比了人工势场(APF)算法、Vortex APF(VAPF)算法、Safe APF(SAPF)算法以及动态窗口(DWA)方法在机器人路径规划中的性能。通过实验,评估了各个算法在不同障碍环境中的表现,尤其是在避障和路径优化方面的差异。实验结果表明,VAPF和SAPF在解决传统APF算法的局部极小值问题上表现优异,而DWA在实时路径规划中具有较好的综合性能。
理论
-
人工势场(APF)算法:基于人工势场算法,机器人在目标点生成吸引力,在障碍物处生成排斥力。通过力的合成引导机器人向目标移动。然而,该算法容易陷入局部极小值,即机器人被困在非目标点的区域。
-
Vortex APF(VAPF)算法:该算法通过引入旋涡场,改进了传统APF的局部极小值问题。机器人不仅受到吸引力和排斥力的影响,还在合适的情况下受到旋转力场的引导,使其更容易逃脱局部极小值区域。
-
Safe APF(SAPF)算法:SAPF算法通过动态调整障碍物周围的排斥力强度,确保机器人在复杂障碍环境中能够安全通行,减少了机器人和障碍物碰撞的风险。
-
动态窗口(DWA)方法:DWA是一种基于速度和加速度的实时路径规划方法。该算法通过评估不同速度和角速度的可行性,找到最优路径,从而实现实时避障和路径规划。DWA方法适用于动态环境,且在计算资源有限的情况下表现优异。
实验结果
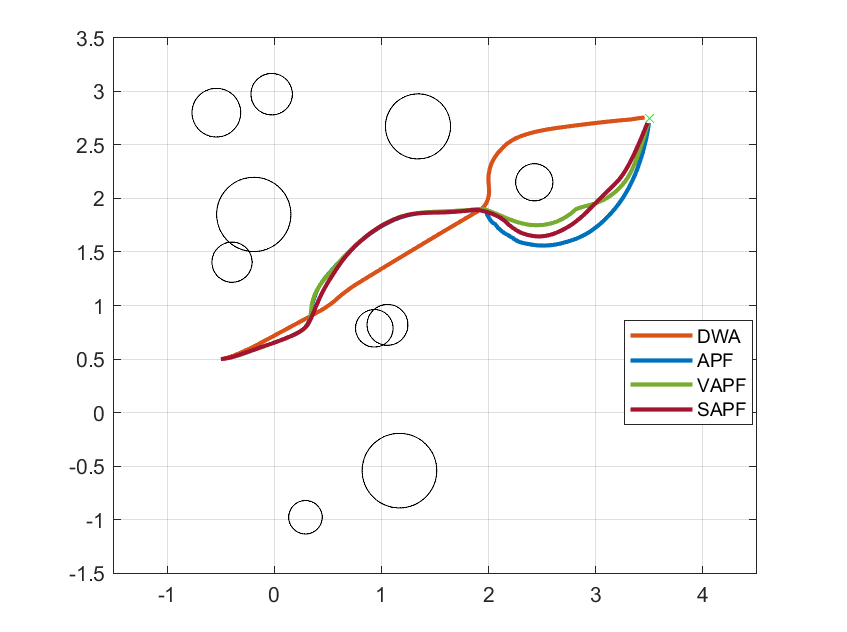
在多个复杂环境下,对比了各算法的表现。下图展示了四种算法的路径规划结果:
-
DWA(橙色):DWA路径较为平滑,避障效果明显,尤其适合实时路径规划。
-
APF(蓝色):APF算法在简单环境中效果较好,但在局部极小值问题上仍有缺陷。
-
VAPF(绿色):VAPF通过旋涡场改进了局部极小值问题,在复杂环境中表现优异。
-
SAPF(红色):SAPF算法在障碍物密集的情况下有更好的避障效果,确保了路径的安全性。
部分代码
-
人工势场算法(APF):
function apf_path = APF(start, goal, obstacles)% 初始化参数k_att = 1.0; % 吸引力系数k_rep = 100.0; % 排斥力系数d0 = 2.0; % 排斥力的作用范围max_step = 1000;apf_path = start;for i = 1:max_steppos = apf_path(end, :);f_att = k_att * (goal - pos); % 吸引力f_rep = [0, 0]; % 初始化排斥力for j = 1:size(obstacles, 1)dist = norm(pos - obstacles(j, :));if dist < d0f_rep = f_rep + k_rep * (1/dist - 1/d0) * (pos - obstacles(j, :)) / dist^3;endendf_total = f_att + f_rep; % 合力new_pos = pos + f_total; % 更新位置apf_path = [apf_path; new_pos];if norm(goal - new_pos) < 0.1 % 如果接近目标点,结束break;endend
end
-
Vortex APF算法(VAPF):
function vapf_path = VAPF(start, goal, obstacles)% 初始化参数k_att = 1.0; % 吸引力系数k_rep = 100.0; % 排斥力系数k_vortex = 10.0; % 旋涡力系数d0 = 2.0; % 排斥力的作用范围max_step = 1000;vapf_path = start;for i = 1:max_steppos = vapf_path(end, :);f_att = k_att * (goal - pos); % 吸引力f_rep = [0, 0]; % 初始化排斥力f_vortex = [0, 0]; % 初始化旋涡力for j = 1:size(obstacles, 1)dist = norm(pos - obstacles(j, :));if dist < d0f_rep = f_rep + k_rep * (1/dist - 1/d0) * (pos - obstacles(j, :)) / dist^3;f_vortex = f_vortex + k_vortex * [-(pos(2) - obstacles(j, 2)), pos(1) - obstacles(j, 1)] / dist^2;endendf_total = f_att + f_rep + f_vortex; % 合力new_pos = pos + f_total; % 更新位置vapf_path = [vapf_path; new_pos];if norm(goal - new_pos) < 0.1 % 如果接近目标点,结束break;endend
end
-
Safe APF算法(SAPF):
function sapf_path = SAPF(start, goal, obstacles)% 初始化参数k_att = 1.0; % 吸引力系数k_rep = 100.0; % 排斥力系数d0 = 2.0; % 排斥力的作用范围max_step = 1000;sapf_path = start;for i = 1:max_steppos = sapf_path(end, :);f_att = k_att * (goal - pos); % 吸引力f_rep = [0, 0]; % 初始化排斥力for j = 1:size(obstacles, 1)dist = norm(pos - obstacles(j, :));if dist < d0% 动态调整排斥力safe_dist = max(0.1, dist);f_rep = f_rep + k_rep * (1/safe_dist - 1/d0) * (pos - obstacles(j, :)) / safe_dist^3;endendf_total = f_att + f_rep; % 合力new_pos = pos + f_total; % 更新位置sapf_path = [sapf_path; new_pos];if norm(goal - new_pos) < 0.1 % 如果接近目标点,结束break;endend
end
-
动态窗口(DWA)算法的核心伪代码:
function dwa_path = DWA(start, goal, obstacles, max_v, max_w)% 初始化max_step = 1000;dwa_path = start;pos = start;v = 0; % 初始速度w = 0; % 初始角速度for i = 1:max_step[v, w] = calculate_velocity(v, w, pos, goal, obstacles, max_v, max_w);pos = update_position(pos, v, w);dwa_path = [dwa_path; pos];if norm(goal - pos(1:2)) < 0.1 % 如果接近目标点,结束break;endend
end
参考文献
❝
Khatib, O. (1986). Real-time obstacle avoidance for manipulators and mobile robots. The International Journal of Robotics Research, 5(1), 90-98.
Fox, D., Burgard, W., & Thrun, S. (1997). The dynamic window approach to collision avoidance. IEEE Robotics & Automation Magazine, 4(1), 23-33.
Park, J. H., & Oh, J. H. (2003). Vortex field method for local path planning of mobile robots. Journal of Intelligent and Robotic Systems, 37(1), 1-16.
Tan, H. S., Zhang, H., & Zhu, Q. (2011). A safe artificial potential field approach for robot path planning. Proceedings of the 2011 International Conference on Information and Automation, 1121-1126.

