【AGC005D】~K Perm Counting(计数抽象成图)
容斥原理。
求出f(m) ,f(m)指代至少有m个位置不合法的方案数。
怎么求?
注意到位置为id,权值为v ,不合法的情况,当且仅当 v = id+k或 v= id-k
因此,我们把每一个位置和权值抽象成点 ,不合法的情况之间连一条边,可以构成二分图。
借用大佬的图。
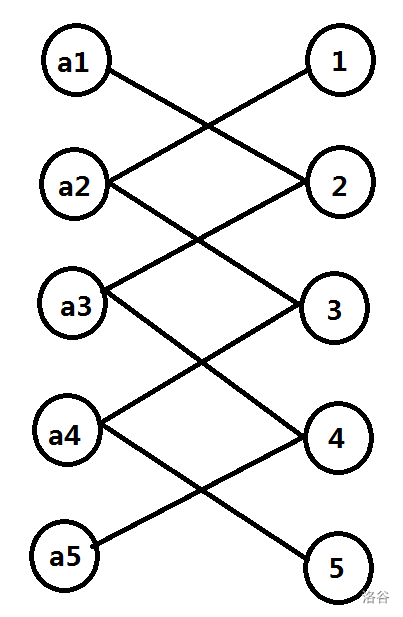
由此可知,当选了n条边,就恰好n个位置不合法,限制条件是:连的边不能相邻,
把二分图展开成k条链,进行dp。
还是借用大佬ez_lcw的图

由此总共有2n 个点 k 条链,链与链之间无边 互不干涉。
dp(i,j,pd)表示考虑到第i号点, 连了j条边,是否有连接i 到 i-1号点。
转移方程
则可得
简单的乘法原理罢了。
#include<bits/stdc++.h>
using namespace std;
long long n,k;
long long fac[4010];
long long dp[4010][4010][2];
int mod = 1e9+7;
int pd[4999];//判断是否为链头 0 表示是头 头不能连接上一个
int main(){freopen("neverk.in","r",stdin);freopen("neverk.out","w",stdout);cin>>n>>k;fac[0] = 1;for(int i = 1;i <= n;i++){fac[i] = (fac[i-1]*(long long)i)%mod;}int tot = 0;for(int i=1;i<=k;i++){for(int t=0;t<2;t++){for(int j=i;j<=n;j+=k){tot++;if(i!=j) pd[tot]=1;}}}dp[0][0][0] = 1;for(int i = 1;i <= 2*n;i++){for(int j = 0;j <= n;j++){dp[i][j][0] = (dp[i-1][j][0] + dp[i-1][j][1])%mod;if(j&&pd[i]) dp[i][j][1] = dp[i-1][j-1][0];}}long long cnt = 0;for(int i = 0;i <= n;i++){//cout<<fac[n-i]<<" "<<dp[2*n][i][0]+dp[2*n][i][1]<<endl;long long t = fac[n-i]*(dp[2*n][i][0]+dp[2*n][i][1]);t%=mod;//cout<<t<<endl;if(i%2 == 0){cnt = (cnt +t)%mod;}else{cnt = (cnt - t + mod)%mod;}}cout<<cnt;return 0;
}