当前位置：首页 > news >正文

求组合数专题

news 2025/7/6 13:46:53

求组合数 Ⅰ（递推公式）

思路 $O(a\cdot b)$

递推法预处理
- 利用公式 $C_{a}^{b} = C_{a-1}^{b-1} + C_{a-1}^{b}$
- 复杂度 $O(a \cdot b) = 4*10^{6}$
直接查询
- 单次查询复杂度 $O(1)$

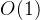
代码

#include <bits/stdc++.h>
using namespace std;
const int N = 2010;
const int mod = 1e9+7;
int c[N][N];
int get_c(int a, int b)
{c[0][0] = 1;for(int i = 1; i <= a; i++){c[i][0] = 1;for(int j = 1; j <= a; j++){c[i][j] = (c[i-1][j-1] + c[i-1][j]) % mod;}}return c[a][b];
}
int main()
{get_c(2000, 2000);int n;cin >> n;while (n -- ){int a, b;cin >> a >> b;cout << c[a][b] << '\n';}
}

求组合数 Ⅱ （乘法逆元、费马小定理、快速幂）

思路 $O(1e5 \cdot log(p-2) + n)$

很明显，递推法预处理会超时。于是我们选择另一种计算组合数的方式：快速幂（处理分子的阶乘、分母的阶乘） + 费马小定理（将除以分母，在模运算中该换为，乘以分母的乘法逆元）
- 步骤
  - 计算阶乘 $O(b_{max}) = 10^{5}$
  - 快速幂求乘法逆元 $O(log(p-2))$ ，p = 1e9+7
- 总复杂度 $O(n \cdot (b_{max} + log(p-2))) > 10^{9}$
- 反思：不同的数据计算阶乘时重复计算了
- 改进：预处理所有阶乘
  - （同时可以预处理所有阶乘的乘法逆元） $O(1e5 * log(p-2))$
- 注意：求 $\frac{a!}{(a-b)!}$ 时仍不能用除法，要采用乘法逆元

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
const int mod = 1e9+7;
typedef long long ll;
ll fac[N], ifac[N];
ll qmi(ll base, ll expo)
{ll retv = 1;while(expo){if(expo & 1) retv = retv * base % mod;base = base * base % mod;expo >>= 1;}return retv;
}
void init()
{fac[0] = ifac[0] = 1;for(ll i = 1; i <= 100000; i++){fac[i] = fac[i-1] * i % mod;ifac[i] = qmi(i, mod-2) * ifac[i-1] % mod;}
}
int main()
{init();int n;cin >> n;while (n -- ){int a, b;cin >> a >> b;cout << fac[a] * ifac[a-b] % mod * ifac[b] % mod << '\n';}
}

求组合数 Ⅲ（卢卡斯定理）

思路

无它，ab值太大了，幸好最后是mod运算，用卢卡斯定理即可
- 条件： p是质数

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
typedef long long ll;
ll qmi(ll base, ll expo, ll mod)
{ll retv = 1;while(expo){if(expo & 1) retv = retv * base % mod;base = base * base % mod;expo >>= 1;}return retv;
}
ll get_c(ll a, ll b, ll mod)
{ll res = 1;for(int i = 1, j = a; i <= b; i++, j--){res = res * j % mod;res = res * qmi(i, mod-2, mod) % mod;}return res;
}
ll lucas(ll a, ll b, ll mod)
{if(a < mod && b < mod)return get_c(a,b,mod);else return get_c(a % mod, b % mod, mod) * lucas(a / mod, b / mod, mod) % mod;
}
int main()
{int n;cin >> n;while (n -- ){ll a, b, p;cin >> a >> b >> p;cout << lucas(a, b, p) << '\n';}return 0;
}

求组合数 Ⅳ（高精度乘法、质因数分解）

思路

阶乘的质因数分解 + 高精度乘法

#include <bits/stdc++.h>
using namespace std;
const int N = 5010;
int primes[N], cnt;
bool st[N];
int s[N];
vector<int> v;
void get_primes(int n)
{for(int i = 2; i <= n; i++){if(!st[i]) primes[++cnt] = i;for(int j = 1; primes[j] * i <= n; j++){st[primes[j] * i] = true;if(i % primes[j] == 0) break;}}
}
int cal(int x, int p)
{int retv = 0;while(x){retv += x/p;x /= p;}return retv;
}vector<int> mul(vector<int> a, int b)
{vector<int> c;int t = 0;for(int i = 0; i < a.size(); i++){t += a[i] * b;c.push_back(t % 10);t /= 10;}while(t){c.push_back(t % 10);t /= 10;}return c;
}
int main()
{get_primes(5000);int a, b;cin >> a >> b;v.push_back(1);for(int i = 1; i <= cnt; i++){int p = primes[i];s[p] = cal(a, p) - cal(a-b, p) - cal(b, p);for(int j = 1; j <= s[p]; j++)v = mul(v, p);}for(int i = v.size()-1; i >= 0; i--) cout << v[i];return 0;
}

查看全文

http://www.mrgr.cn/news/40148.html