矩阵转置的运算公式来了，附矩阵转置计算器

大家好，这里是效率办公指南！

📊 矩阵转置是线性代数中的一个基本概念，它将矩阵的行和列互换。这不仅是理论数学中的一个操作，也是数据分析和计算机科学中常用的技巧。今天，我们将详细介绍矩阵转置的公式、方法，并提供一些计算示例。

矩阵转置的公式

设有一个  M x N  的矩阵  A  ，其转置矩阵  A^T  是一个  N x M  的矩阵，转置操作将矩阵  A  的行列互换。具体来说，矩阵  A  中的元素  a_ij  将变为  A^T  中的元素  a_ji  。

矩阵转置的方法

方法一：直接交换行列

1. 确定转置矩阵的大小：原矩阵  A  是  M x N  ，则转置矩阵  A^T  为  N x M  。

2. 交换行列：将  A  的第  i  行第  j  列的元素  a_ij 移到  A^T  的第  j  行第  i  列。

方法二：使用数学公式

对于矩阵  A  中的任意元素  a_{ij}  ，其转置矩阵  A^T  中对应的元素可以通过以下公式得到：

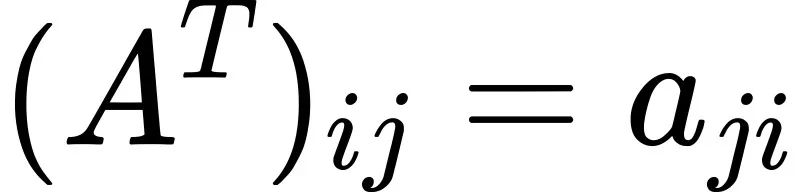
计算示例

示例一：二阶矩阵转置

考虑以下二阶矩阵 A

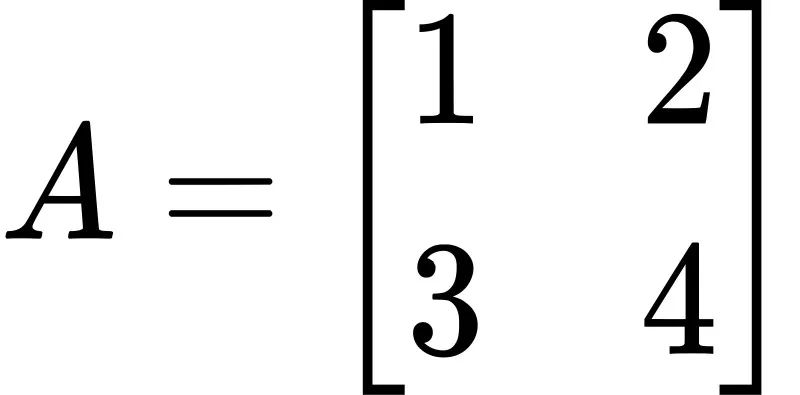
其转置矩阵为：

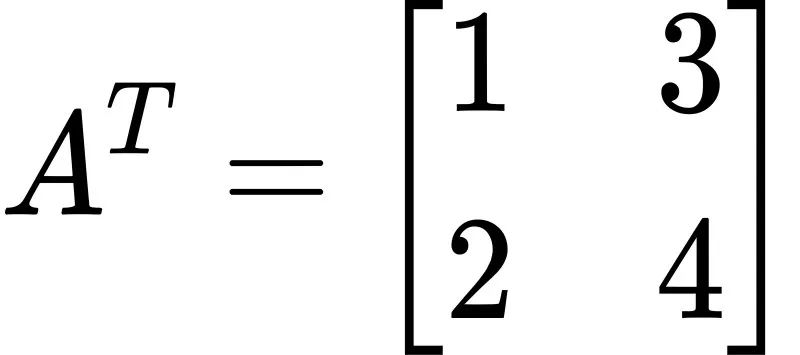
示例二：三阶矩阵转置

考虑以下三阶矩阵

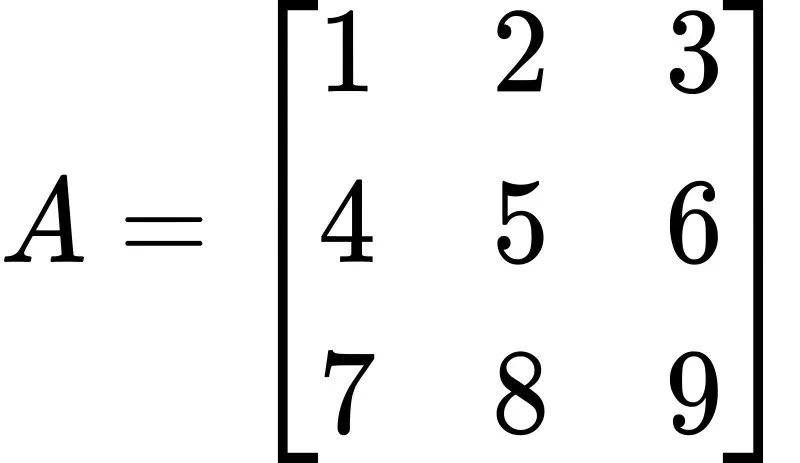
其转置矩阵为：

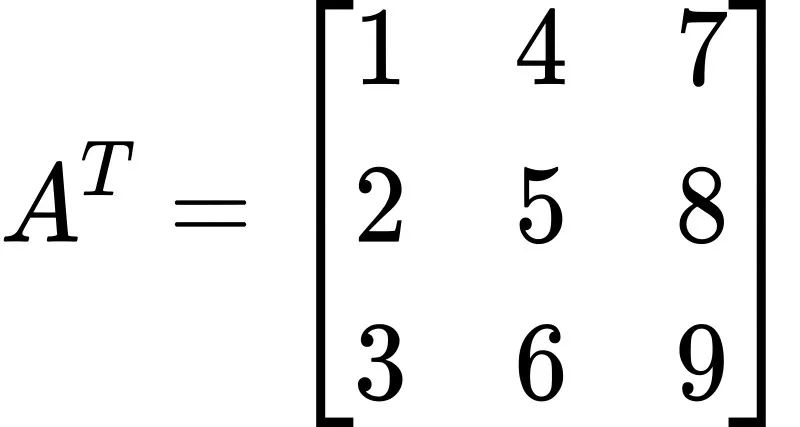
示例三：非方阵矩阵转置

考虑以下非方阵矩阵（2行3列）：

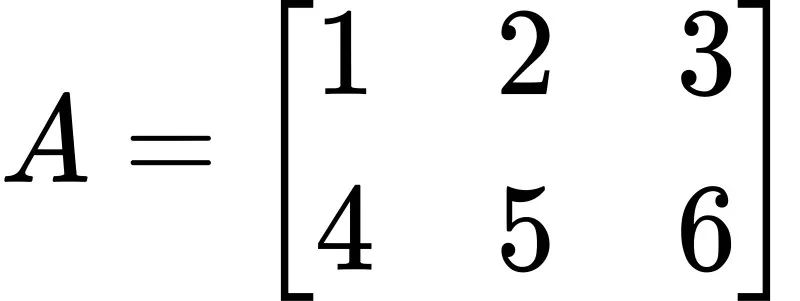
其转置矩阵为（3行2列）：

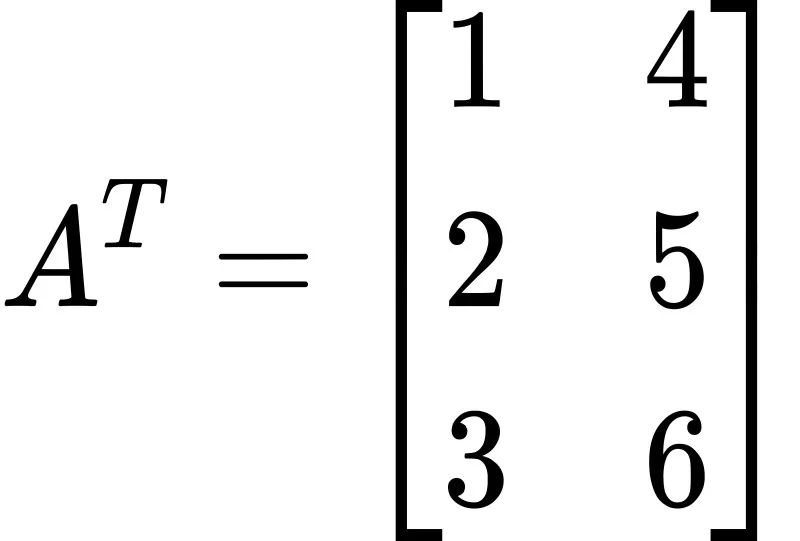
注意事项

• 矩阵转置操作不会改变矩阵元素的值，只改变元素的排列方式。

• 转置操作可以视为矩阵乘以自身的伴随矩阵。

• 矩阵转置是逆序的，即 (A^T)^T = A 

总结

矩阵转置是线性代数中的一个基础且重要的操作。掌握矩阵转置的公式和方法，可以帮助我们更好地理解和处理矩阵数据。如果你有任何疑问或需要进一步的帮助，欢迎在下方留言，我们会尽快为你解答。

微信搜一搜【智启创想】，使用矩阵转置计算器