5.5树与二叉树的应用

5.5.1哈夫曼树和哈夫曼编码

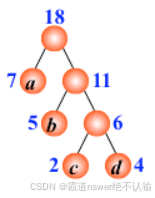
1.哈夫曼树的定义

路径长度:路径上的分支书目

权值:被赋予某种意义的值

带权路径长度=路径长度*权值

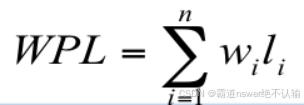
最优二叉树/哈夫曼树:n个带权叶节点的二叉树中,带权路径长度wpl最小的二叉树为哈夫曼树

2.哈夫曼树的构造

将权值最小的放到最下面

性质:构建过程中共新建了n-1个节点,因此哈夫曼树的节点总数为2n-1;

哈夫曼树中不存在度数为1的接节点;

3.哈夫曼编码

哈夫曼编码是一种非常有效的数据压缩编码

根据数据的权重来构造哈夫曼树

5.5.2并查集

并查集的逻辑结构:集合

存储结构:树的双亲存储---双亲存储方便找到节点的双亲节点

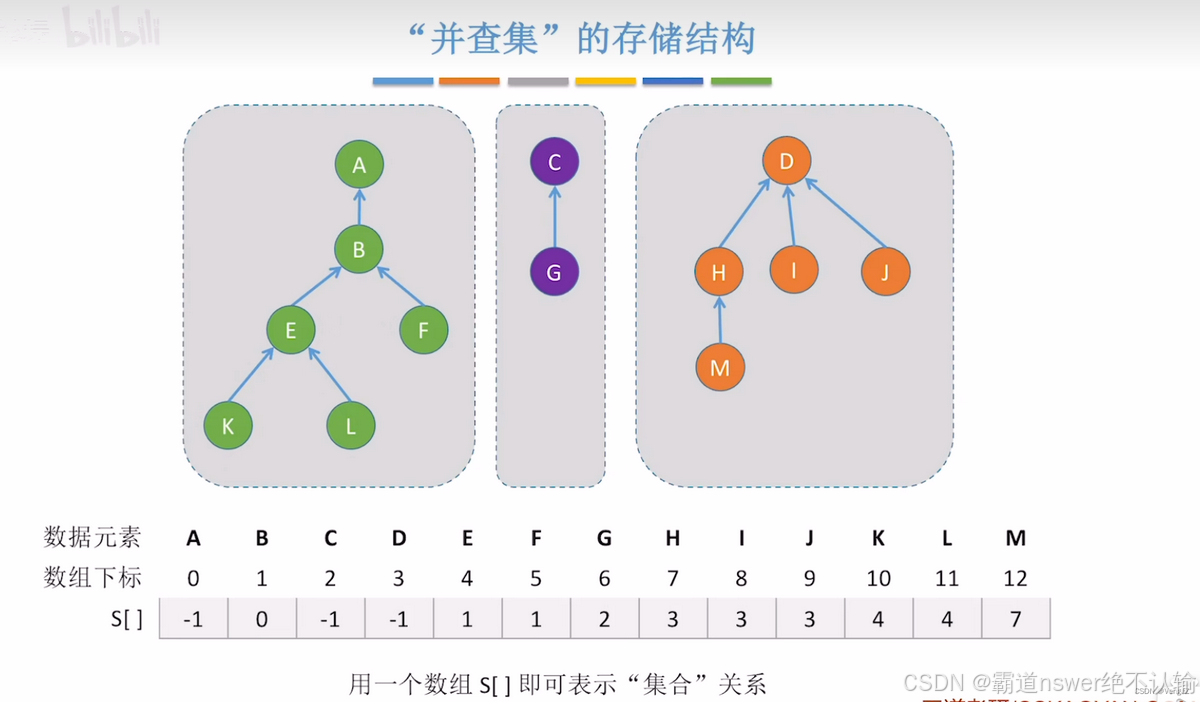
1.并查集的基本实现

结构定义

#define size 100
int UFsets[size];//定义一个集合元素数组

初始化

//并查集初始化操作
void initial(int s[]) {for (int i = 0; i < size; i++){s[i] = -1;//每个自动成单元素集合}
}

Find操作

查找并返回包含元素x的根

//Find操作--查找根节点
int find(int s[],int x) {//s[]集合,x目标元素下标int root = x;while (root!=-1)	//循环寻找x的根{root = s[root];}return root;
}

Union操作

求两个不想交子集和的并集

//Union操作--合并两个不想交子集
void Union(int s[],int root1,int root2) {//s[]集合,root1--根1,root2--根2//判断两根是否不同if (root1 == root2) return;//两根相同s[root2] = root1;//两根不同--将根2连接到根1下面
}

Find时间复杂度为o(d);

Union时间复杂的度为o(1);\

2.并查集实现的优化

核心思想:尽可能让树变矮

改进Union的操作

1)用根节点绝对值表示树的节点总数

2)union操作让小树合并成大树

void Union(int s[], int root1, int root2) {//s[]集合,root1--根1,root2--根2//用根节点的绝对值表示树的节点总数//union操作让小树合成大树if (s[root2]>s[root1])//root1长度>root2长度{//root2合成入root1中root1 += root2;//累加集合树的节点总数s[root2] = root1;}else {root2 += root1;//累加集合树的节点总数s[root1] = root2;//root1合并入root2中;}}

改进Find操作

1)先找到根路径

2)压缩路径-向上找根,经过的node都直接挂载到根节点处

//Find操作--查找根节点
int find(int s[], int x) {//s[]集合,x目标元素下标
//查找x的根节点int root = x;//记录根节点while (root>=0){root = s[root];}
//x到根经过的节点都直接指向根节点while (x!=root) {int t = s[x];s[x] = root;x = t;}return root;
}