Nature:最大扩散强化学习
转自:清熙
强化学习(RL)智能体(Agent)常常很难在现实世界中广泛部署:初始化差异影响大,样本效率低下,情境之外难以泛化。
研究发现问题的关键是违反了数据独立同分布 (iid) 的假设,而 iid 是大多数机器学习的基础。
强化学习(特别是具身)智能体的经验不可避免是连续的,且跨时间点相关,这也是笔者强调的RL的非马尔可夫性 。
昨日,Nature机器智能,发文“最大扩散强化学习(MaxDiff RL)”解决了此问题。
图片
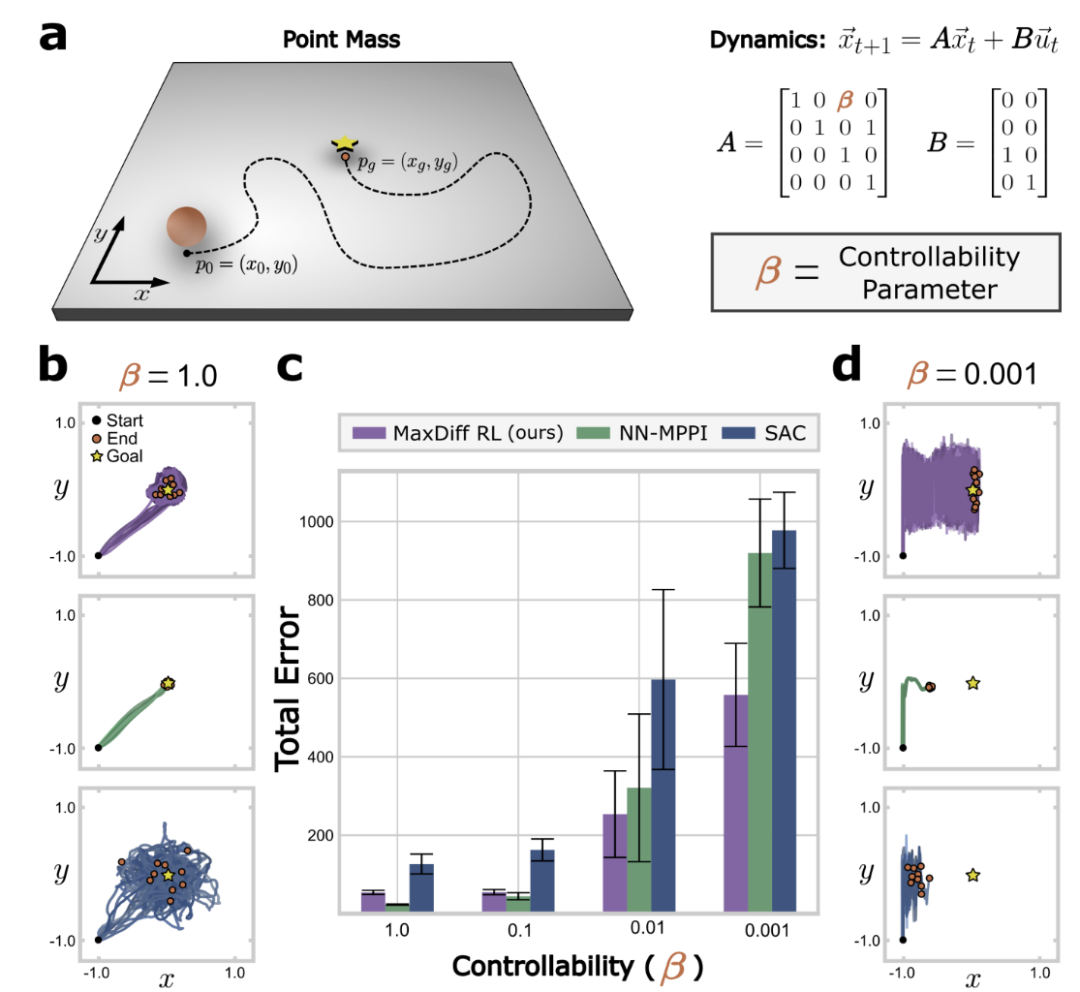
图1:时间相关性破坏了强化学习的SOTA技术,对于大多数系统,可控属性决定了状态转换之间的时间相关性。
强化学习领域的大多数方法都假设随机行为会产生有效的探索,最大熵强化学习(MaxEnt RL)这样的高级技术,也隐含这一假设。
不同于从固定的均匀分布或高斯分布中采样,最大熵强化学习最大化学习到的路径分布(即策略)的熵,以期确保足够的随机性来改善探索。
而实际是否可行,取决于智能体的可控属性,与其引发的时间相关性。状态转换之间的时间相关性可能会阻碍有效探索,严重影响深度强化学习智能体的性能。
图片
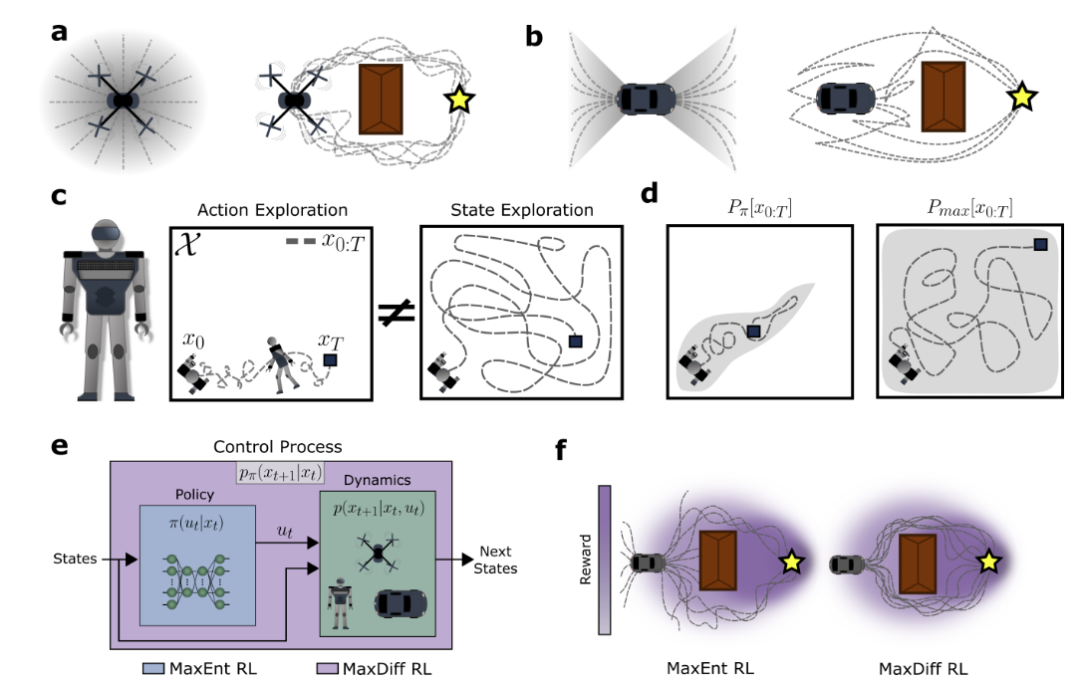
图2:最大扩散RL缓解了时间相关性以实现有效的探索。a、b,具有不同平面可控属性的系统。c,行动随机化是否导致有效的状态探索取决于基础状态转移动力学的属性。
论文从最大熵原理的统计力学中汲取灵感,该原理是最大口径变分优化,在连续性或时间关联约束下,优化目标是找到轨迹分布Pmax[x(t)], 优化一个熵函数S[P[x(t)]]。
幸运的是,这个受限变分优化问题对于最大熵路径分布具有解析解,其中Z是一个归一化常数:
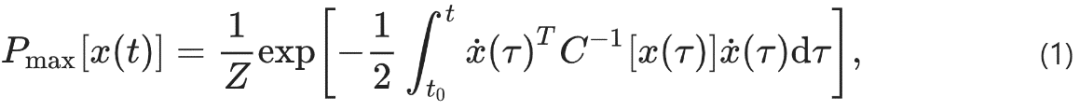
图片
满足遍历性对最终智能体的性质具有深远的影响。遍历性是动力系统的一个正式属性,保证了单个轨迹的统计量在渐近情况下等同于大量轨迹的统计量。
尽管强化学习智能体时间相关性使得iid采样不可行,遍历性强化学习智能体的全局统计量与iid采样的统计量却无法区分。
图片
图3:最大扩散RL智能体对随机种子和初始化具有鲁棒性。
最大扩散强化学习核心是找到一个能够满足最大扩散路径统计的策略(policy),一个policy 意味着一个轨迹分布。
找到满足最大扩散的轨迹分布的policy,是一个优化问题:最小化“agent现在的轨迹分布与 最大扩散轨迹分布“之间的KL距离。
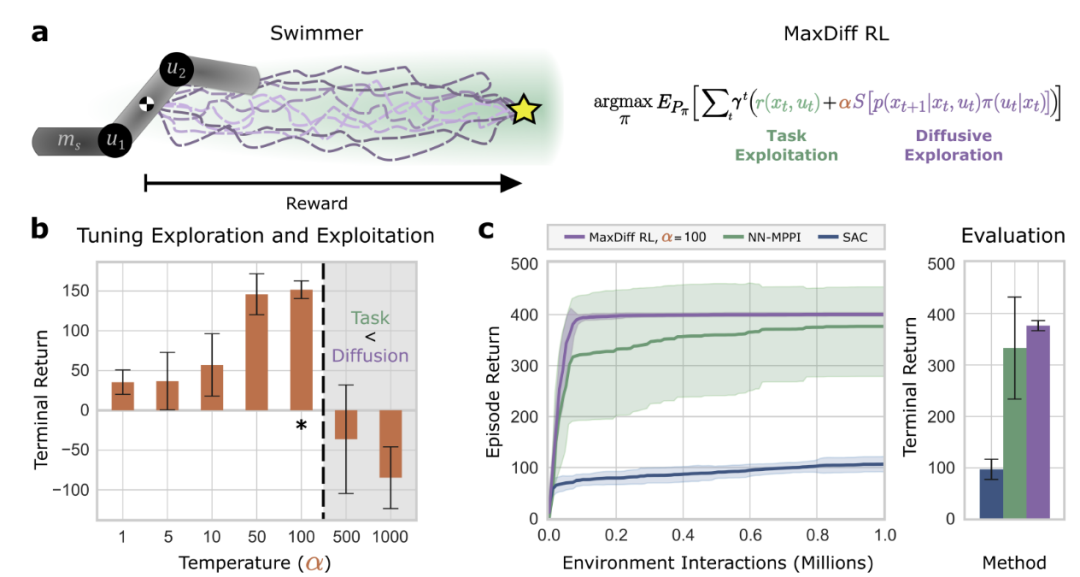
此KL距离可被写成等效的随机最优控制问题,目标是找到一种policy,最大化“智能体在环境中累计奖励的数学期望”。α>0是超参,用于平衡扩散探索和奖励。
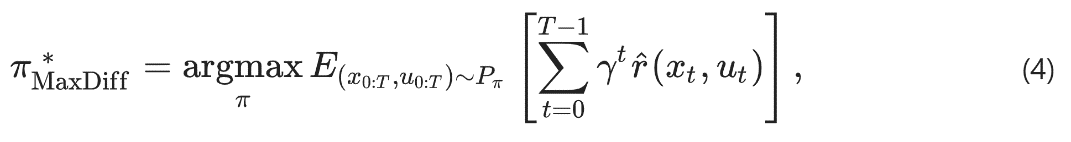
图片
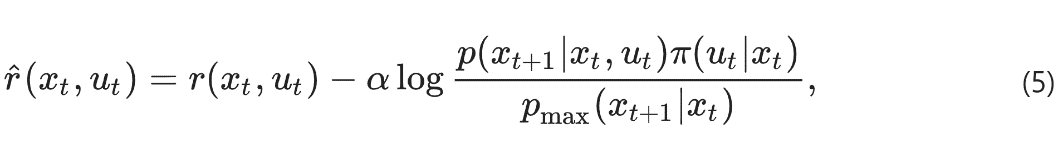
图片
智能体路径熵的局部估计则可以从观察中学习到:
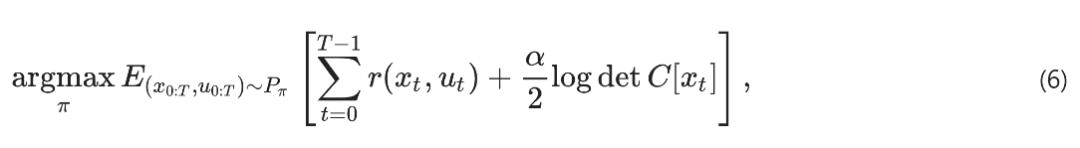
图片
图片
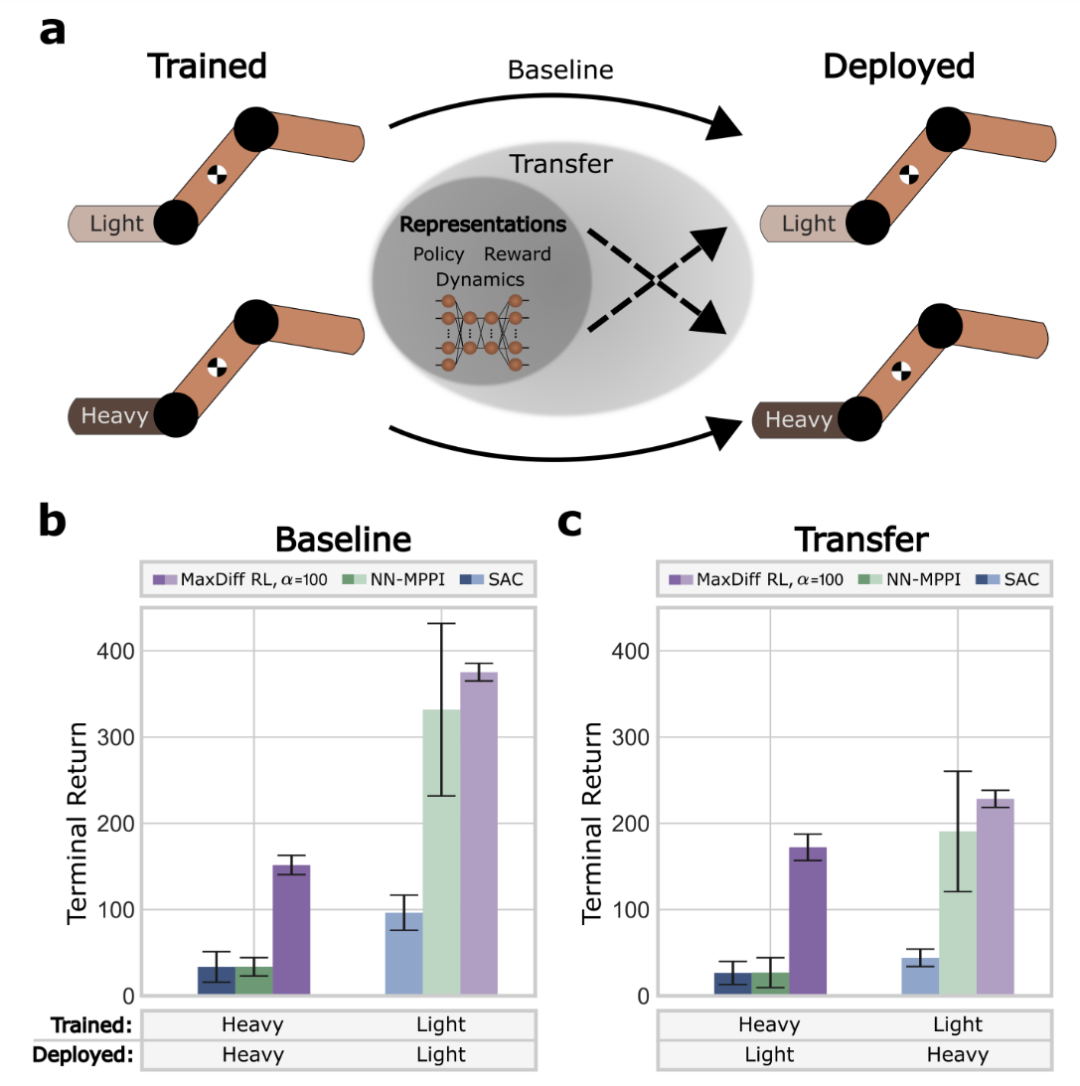
图4:训练系统的具身性确定了部署系统的性能。
MaxDiffRL 同时考虑策略和智能体-环境动力学的时间相关性的一般形式,若不考虑时间相关性,就褪化成MaxEntropy,即MaxEnt是MaxDiff的特例。
图片
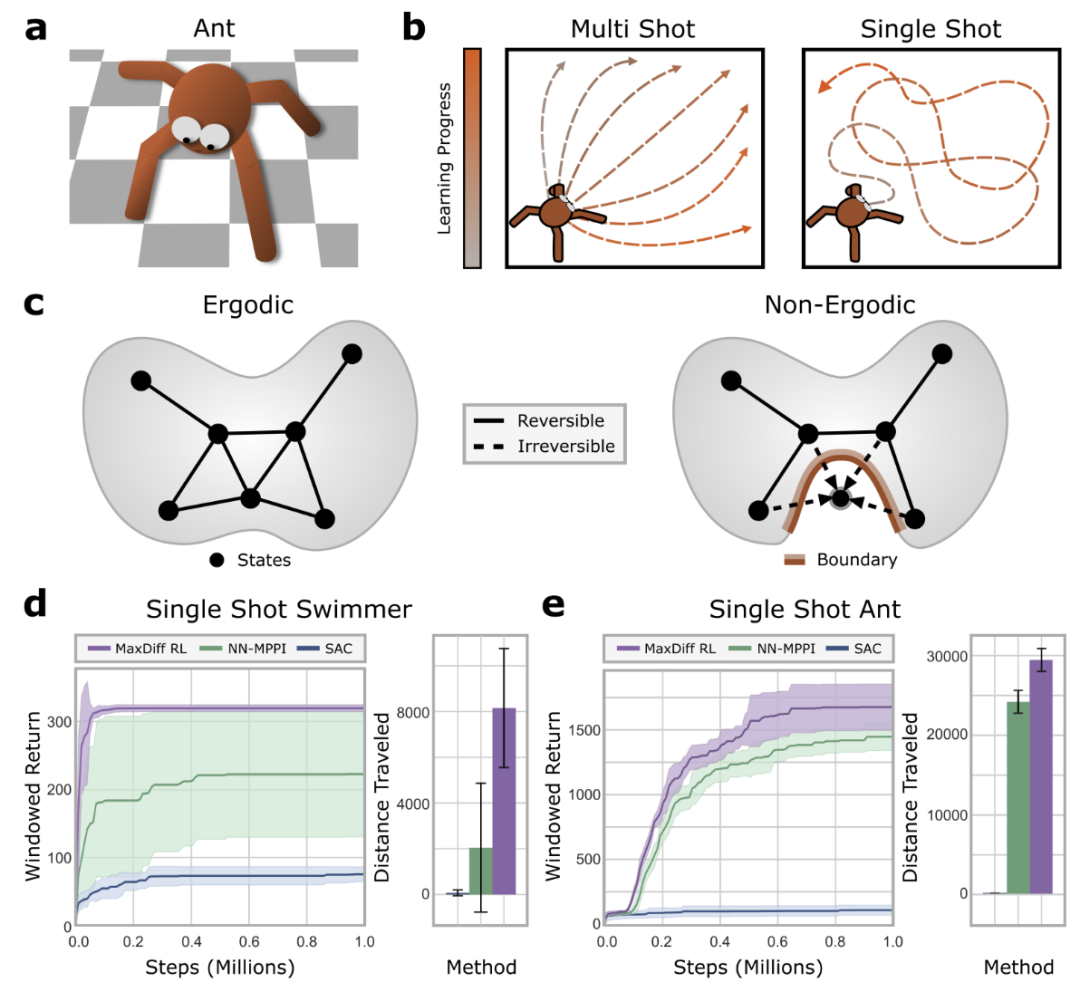
图5:最大扩散RL智能体能够进行单次学习。
验证表明,MaxDiffRL方法针对初始化具有鲁棒性,实现了高效单样本学习,情境之外也易于泛化。
流行的基准测试中,MaxDiffRL也稳健地超越了SOTA。为强化学习智能体(如运动机器人和自动驾驶汽车)的更透明更可靠的决策奠定了基础。
SORA 学习到物理原理,看起来也可以以某种方式借鉴MaxDiffRL 类似的方法,以更好的处理时空碎片状态空间时间相关性,更好把控其动态性。
点击阅读原文链接 https://www.nature.com/articles/s42256-024-00829-
