【机器学习入门】一文读懂线性支持向量机SVM

一 背景

在前面【机器学习入门】一文读懂线性可分支持向量机中 ，线性可分支持向量机主要解决了两个问题：当数据线性可分时，直接使用最大间隔的超平面划分；当数据线性不可分时，则通过核函数将数据映射到高维特征空间，使之线性可分。然而在现实问题中，对于某些情形还是很难处理，例如数据中有噪声的情形，噪声数据（outlier）本身就偏离了正常位置，但是在前面的SVM模型中，我们要求所有的样本数据都必须满足约束，如果不要这些噪声数据还好，当加入这些outlier后导致划分超平面被挤歪了，如下图所示，对支持向量机的泛化性能造成很大的影响。

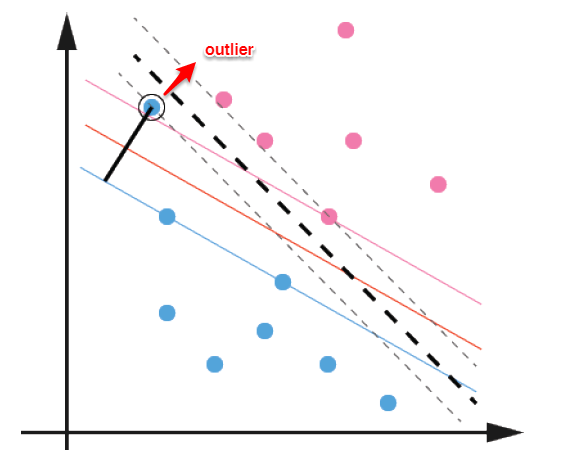
为了解决这一问题，我们需要允许某一些数据点不满足约束，即可以在一定程度上偏移超平面，同时使得不满足约束的数据点尽可能少，这便引出了**“软间隔”支持向量机**的概念

* 允许某些数据点不满足约束y(w'x+b)≥1；
* 同时又使得不满足约束的样本尽可能少。

二 原理

根据背景中的分析我们知道，对于这样的数据，线性可分支持向量机的问题是约束$y_i(w^T{x}_i+b)\ge 1$太“硬”，太严格，数据无法满足，那么如果我们把约束放宽松一点呢？我们把约束变为：
$$y_i(w^T{x}_i+b)\ge 1-{\xi }_i，{\xi }_i\ge 0$$
式中， ${\xi }_i$是松弛变量，顾名思义它将约束条件变得宽松了，这样那些异常点也可以满足约束了，但是其${\xi }_i$会比较大，也就是要多“宽松”一些，如下图所示，松弛变量表示了异常点到间隔边界的函数间隔：

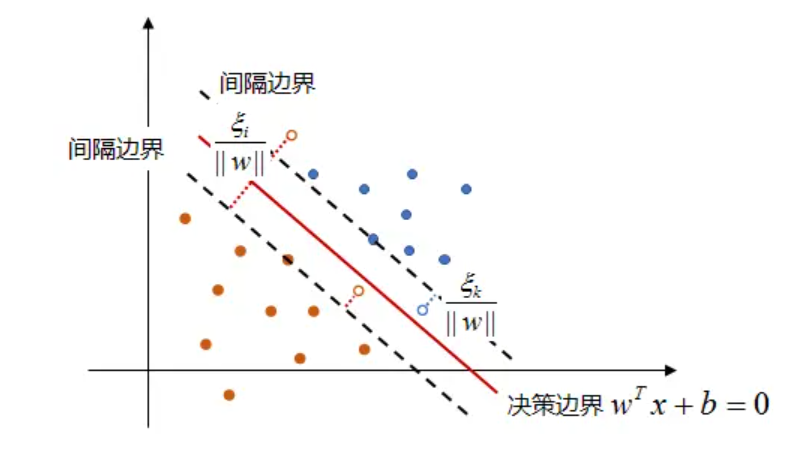
问题是，约束变得宽松了怎么能保证分类的效果呢？要知道支持向量机的优势就是其严格的约束使得分类超平面与两个类别间隔最大且相等，为了弥补约束放松的缺点，引入“代价”${\xi }_i$，即放松了多少约束，就有承受多大的代价，因此目标函数变为：
$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\xi }_i \\ s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i，{\xi }_i\ge 0,i=1,2,...,m \end{gathered}$$
式中，$C>0$是惩罚参数，$C$越大对异常点的惩罚越大，约束越严格，$C$的具体取值由实际应用决定。这里的目标函数既要使$\frac{1}{2}||w|{|}_2^2$尽量小即间隔尽量大，又要使满足约束的样本尽量多即误分类点尽量少，这两个目标使互相矛盾的，由$C$来控制二者的强弱关系。

综上所述，对于有噪音的线性不可分数据，我们选择放松其约束，相对于基于严格约束的硬间隔最大化来说，这种做法称为软间隔最大化，解决这种线性不可分数据的分类问题，基于软间隔最大化的支持向量机称为线性支持向量机（看名字也能感受到线性支持向量机应该包含线性可分支持向量机，线性可分支持向量机是松弛变量都为0的线性支持向量机特例）。

线性支持向量机模型：
$$f(x)=sign(w^{\ast }x+b^{\ast })$$
$w^{\ast }x+b^{\ast }=0$为决策超平面，线性支持向量机看起来与线性可分支持向量机一样，只是在决策超平面的计算思路上有些不同。

三 支持向量机模型求解

3.1 目标函数

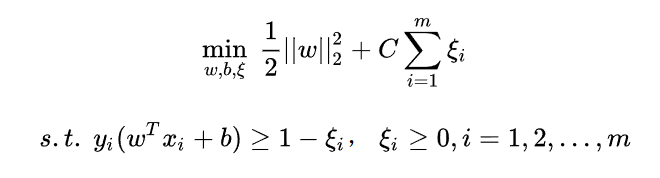
3.2 转换为对偶问题

转化过程与【机器学习入门】一文读懂线性可分支持向量机是一样的，首先是拉格朗日乘子法：

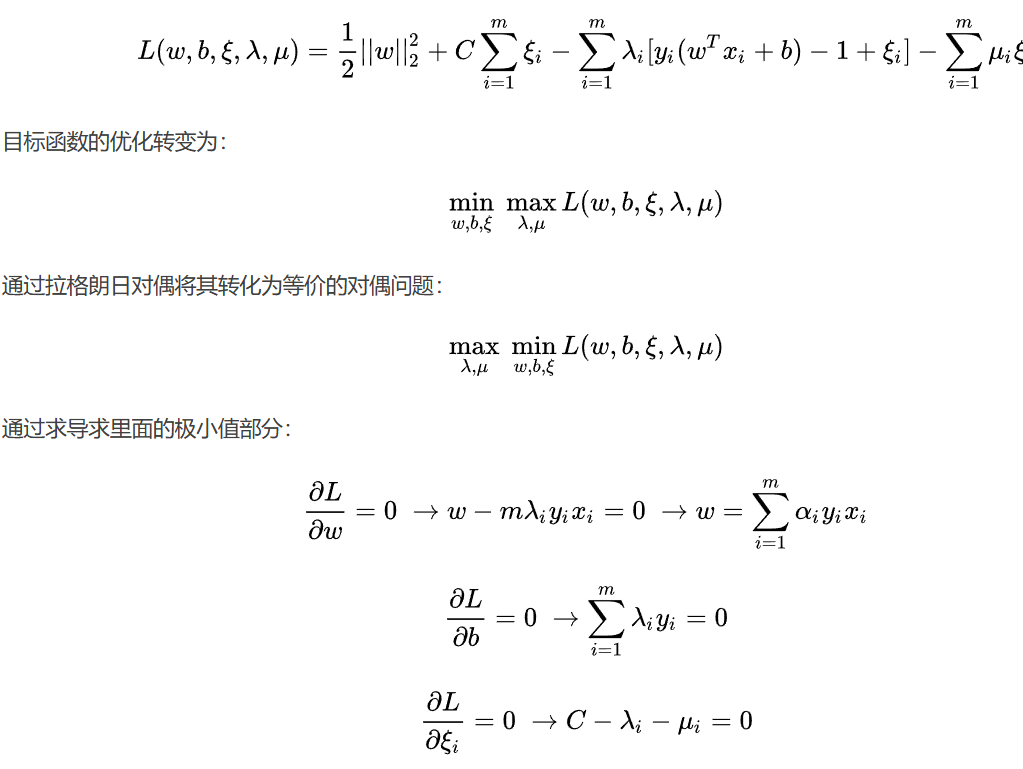
代入公式可得：

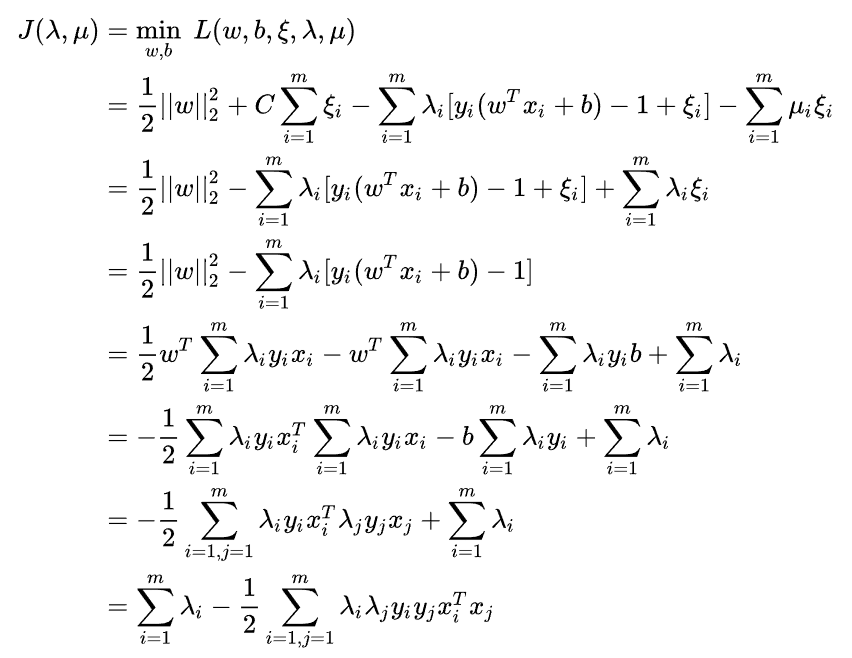
以上这些推导的每个步骤处理的原理就不细说了，想弄明白的话可以看上一篇【机器学习入门】一文读懂线性可分支持向量机

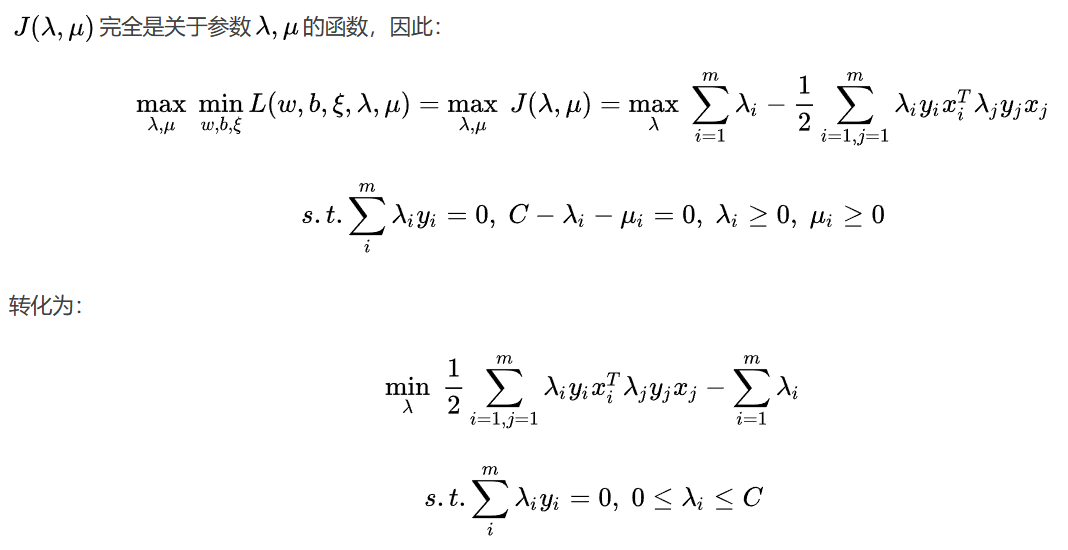
与线性可分支持向量机基本上是一样的，只是约束不同，求出上式取得极小值时对应的$\lambda$向量就可以求出$w$和$b$了，这里同样需要用到SMO算法来求$\lambda$。

3.3 线性支持向量机的算法过程