NOI2003 逃学的小孩 题解
NOI2003 逃学的小孩 题解
传送门。
题目简述
给定一棵树 T T T,需要选择三个点 A , B , C A,B,C A,B,C,需要从 C C C 走到 A , B A,B A,B 的最远距离。
(第一段题目是在讲剧情吗。。)
前置知识
- 图
- 树
- 树的直径
思路简述
这题在蓝题(提高+ / 省选-)中还是比较水的 ^_^
来看看样例吧
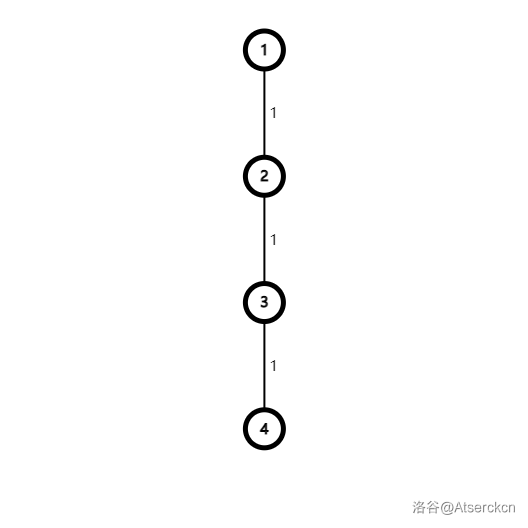
用瞪眼法(——数学老师) 看看,发现 A , B A,B A,B 可以设在 1 1 1 和 4 4 4,然后 C C C 在 2 2 2 或 3 3 3 都无所谓。
那么 4 4 4 是咋来的呢?
(设 C C C 在 2 2 2)
2 → 1 → 4 2\rightarrow 1 \rightarrow4 2→1→4。
由于是最远距离,那么——
树的直径!
而刚好,树的直径就是有两个端点,刚刚好可以一个作为 A A A,一个作为 B B B。
然后 C C C 就是在除了 A , B A,B A,B 的节点,距离 A , B A,B A,B 的最短路径。
那么,直接枚举所有 C C C,取最大值再加上 A → B A\rightarrow B A→B 的距离(直径距离)即可。
代码实现
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=2e5+5;
ll n,m,head[N],cnt_e,u,v,w,top,dis_start[N],dis_stop[N],start,stop,ans,ans2;
struct E{ll from,to,w,pre;
}e[N<<1];
inline void add(ll from,ll to,ll w)//链式前向星
{e[++cnt_e].from=from;e[cnt_e].to=to;e[cnt_e].w=w;e[cnt_e].pre=head[from];head[from]=cnt_e;return;
}
void dfs_d(ll u/*当前节点*/,ll fa/*他爹*/,ll sum/*目前的最长路径*/)//求树的直径
{if(sum>ans)ans=sum,top=u;for(ll i=head[u];i;i=e[i].pre){ll v=e[i].to;if(v==fa) continue;dfs_d(v,u,sum+e[i].w);}return;
}
void dfs_dis_start(int u,int fa)//所有点到某个端点的距离
{for(ll i=head[u];i;i=e[i].pre){ll v=e[i].to;if(v==fa) continue;dis_start[v]=dis_start[u]+e[i].w;dfs_dis_start(v,u);}return;
}
void dfs_dis_stop(int u,int fa)//所有点到另一个端点的距离
{for(ll i=head[u];i;i=e[i].pre){ll v=e[i].to;if(v==fa) continue;dis_stop[v]=dis_stop[u]+e[i].w;dfs_dis_stop(v,u);}return;
}
signed main(){scanf("%lld%lld",&n,&m);for(ll i=1;i<=m;i++){scanf("%lld%lld%lld",&u,&v,&w);add(u,v,w);add(v,u,w);}dfs_d(1,0,0);start=top;ans=0;dfs_d(start,0,0);stop=top;dfs_dis_start(start,0);dfs_dis_stop(stop,0);for(ll i=1;i<=n;i++)//枚举所有可能的Cans2=max(ans2,min(dis_start[i],dis_stop[i]));printf("%lld\n",ans+ans2);//ans:直径距离//ans2:某个点到两个端点的最短距离return 0;
}
小彩蛋
我:不对劲,有问题:
1 ≤ T i ≤ 1 0 9 1\le T_i \le 10^9 1≤Ti≤109
十亿分钟。。。先不说你能不能活到那时候,就算能考试貌似就已经结束了吧。。
