机器学习——支持向量机

一、间隔与支持向量

  给定训练样本集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x m , y m ) } , y i ∈ { − 1 , + 1 } D=\{ (\bm x_1,y_1),(\bm x_2,y_2),\cdots,(\bm x_m,y_m)\},y_i \in \{ -1,+1\} D={(x1​,y1​),(x2​,y2​),⋯,(xm​,ym​)},yi​∈{−1,+1}，分类学习最基本的想法就是基于训练集$D$在样本空间中找到一个划分超平面，将不同类别的样本分开。
  如图所示，可能存在的划分超平面的样本有很多，直观上看，应该去找位于两类训练样本“正中间”的划分超平面。这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化性能最强。

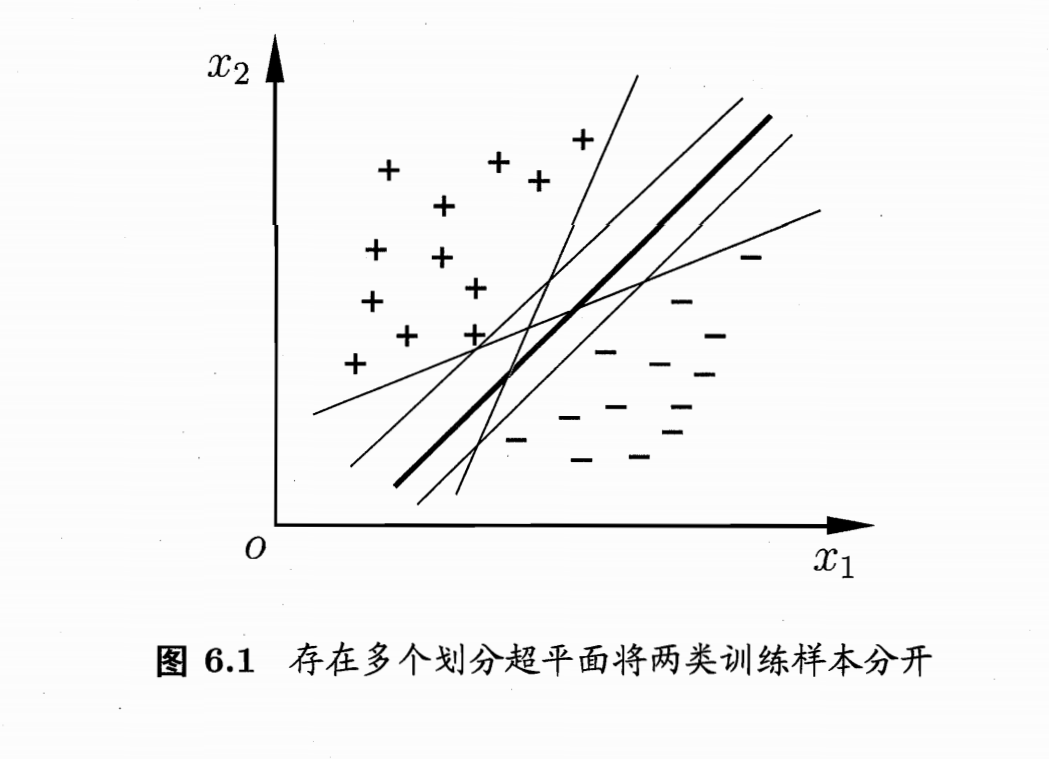
  在样本空间中，划分超平面可以通过如下线性方程来描述：
$${\mathbf{W}}^T\mathbf{x}+b=0$$
其中，$\mathbf{w}=(w_1;w_2;\cdots ;w_d)$为法向量，决定了超平面的方向，$b$为位移项，决定了超平面与原点之间的距离。样本空间中任意点$\mathbf{x}$到超平面$(\mathbf{w},x)$的距离可以表示为
$$r=\frac{|{\mathbf{w}}^T+b|}{||\mathbf{w}||}$$
  假设超平面$(\mathbf{w},b)$能将训练样本正确分类，即对于$(\mathbf{w},b)\in D$，若$y_i=+1$，则有${\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}+b>0$;若$y_i=-1$，则有${\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}+b<0$.令
$$\{\begin{array}{l}{\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}+b\ge +1,y_i=+1;\\ {\mathbf{w}}^{\mathbf{T}}{\mathbf{x}}_{\mathbf{i}}+b\le -1,y_i=-1\end{array}$$
  距离超平面最近的这几个训练样本点使上式的等号成立，它们被称为“支持向量”，两个异类支持向量到超平面的距离之和为
$$\gamma =\frac{2}{||\mathbf{w}||}$$

$\gamma$被称为“间隔”

  如要找到具有“最大间隔”的划分超平面，也就是要找到能满足上式中约束的参数$\mathbf{w}和b$，使得$\gamma$最大。
$$\{\begin{array}{l}ma{x}_{\mathbf{w},b}\frac{2}{||\mathbf{w}||}\\ s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,\cdots ,m.\end{array}$$
  由上式可知，为了最大化间隔，仅需最大化$||\mathbf{w}|{|}^{-1}$，等价于最小化$||\mathbf{w}|{|}^2$，则上式可以重新写为
$$\{\begin{array}{l}mi{n}_{\mathbf{w},b}\frac{1}{2}||\mathbf{w}|{|}^2\\ s.t.y_i({\mathbf{w}}^T{\mathbf{x}}_i+b)\ge 1,i=1,2,\cdots ,m.\end{array}$$
  　这就是支持向量机SVM的基本型

后续内容由于准备的不充分，将写在其他博客中。