● 1049. 最后一块石头的重量 II

题目要把石头分成两堆，这两堆的重量差值最小。相撞之后剩下的石头重量就最小。其实就是要尽量把石头分为差不多重量的两堆，和昨天的● 416. 分割等和子集相似，这样就转换成了01背包问题。

和416题一样，背包里面放的是两堆其中一堆的石头，需要尽量装满sum/2，其中一堆越接近sum/2，两堆石头重量就越差不多。所以这里价值和重量是等同的 ，weight数组就是stones数组，value数组也是stones数组。容量begweight就得取sum/2。

代码如下，注意最后返回的是另一堆的重量减去背包里的重量，因为背包重量≤sum/2，所以另一堆重量≥背包重量。

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum=0;for(int a:stones)sum+=a;//求和int begweight=sum/2;//背包容量vector<int> dp(begweight+1,0);  //已初始化for(int i=0;i<stones.size();++i){for(int j=begweight;j>=stones[i];--j){dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]); //weight和value数组都是stones}}return (sum-2*dp[begweight]);   //dp[begweight]是背包里的重量}
};

● 494. 目标和

在每个数前面要么添加"+"，要么添加"-"，所以也是分为两堆：设为left和right。添加"+"的是left，添加"-"的是right。

有：left-right=target；left+right=sum。

所以left=(sum+target)/2。其中sum和target都已知，所以left可知，问题就是在集合nums中统计和为left的组合数量。所以背包容量应该为left的值。

有两个情况可以直接返回：如果sum+target的和是奇数，那left是不存在的，返回0；如果target的绝对值比sum还大，怎么添加"+"和"-"都不会得到left，也返回0.

动归五部曲：

1. DP数组及其下标的含义。dp[j]：装满容量为j的包，有dp[j]种方法。

所以和昨天的不同，这个是装满容量为j，所以背包容量直接就是j，昨天的是最大容量为j。而且这个是组合问题。所以五部曲得重新思考。

2. 递推公式。dp[j]背包现在容量是j，考虑最后放入的物品，有可能是小于等于j的物品中的任意一个，那么对于所有的nums[i]≤j，都可能是最后一步放入的。所以放一个其中的nums[i]，对应的方法数应该是dp[j-nums[i]]。所以统计dp[j]就得考虑所有的小于j的nums[i]在背包里面的情况，那么就需要把所有的dp[j-nums[i]]加起来，才是dp[j]的值。例子如下：

dp[j]，j 为5。如果小于j的nums[i]有1,2,3,4,5，那么5种情况，都考虑，然后一起加上。

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包。
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包。
• 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包。

所以

这个公式在后面背包解决排列组合问题的时候还会用到。

3. DP数组如何初始化。dp[0] 需要= 1，虽然=1不好解释，但是如果初始化为0的话，之后怎么加结果都只会是0，所以肯定是不行的。

4. 遍历顺序。昨天滚动一维数组中说过的，先物品再背包，而且背包要倒序。

5. 打印DP数组。动手模拟，输出检查。

输入：nums: [1, 1, 1, 1, 1], S: 3

bagweight = (S + sum) / 2 = (3 + 5) / 2 = 4

dp数组状态变化如下：

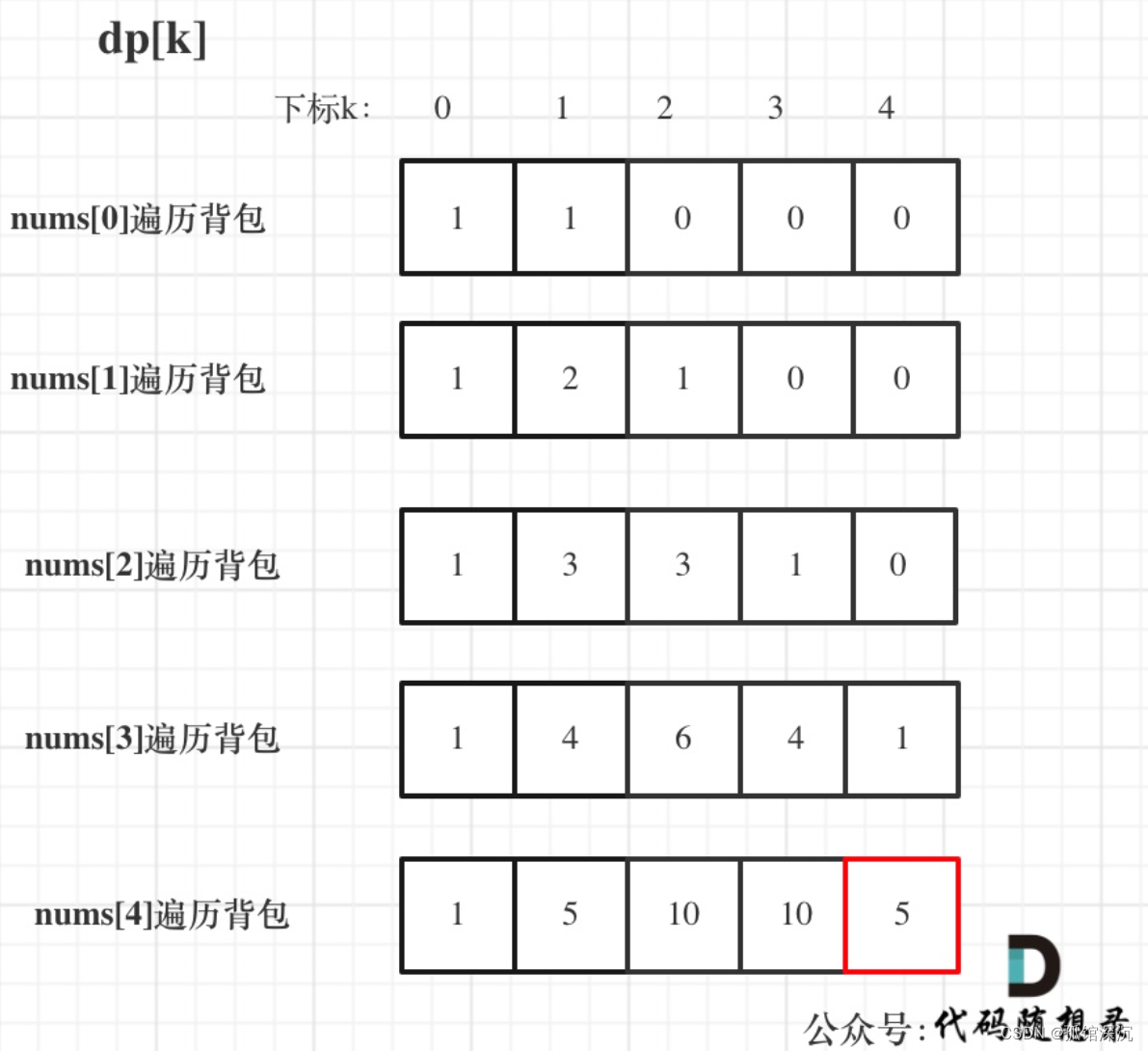
代码：

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum=0;for(int a:nums)sum+=a;//2种没有结果的情况if(abs(target)>sum)return 0;if((sum+target)%2==1)return 0;//背包容量begweight=left=(sum+target)/2int begweight=(sum+target)/2;vector<int> dp(begweight+1,0);//不能是0.dp[0]=1;for(int i=0;i<nums.size();++i){for(int j=begweight;j>=nums[i];--j){dp[j]+=dp[j-nums[i]];}}return dp[begweight];}
};

● 474.一和零

输入有m和n，输出包含m个0和n个1的子集的最大长度。那么dp数组应该有两个维度，最后应该返回dp[m][n]。

动规五部曲：

1. DP数组及其下标的含义。

dp[i][j]：背包里面有 i 个0和 j 个1，可以最多装下dp[i][j]个物品（集合）。

2. 递推公式。

每个物品的重量/价值也应该是两个维度：x个0和y个1。所以有value0和value1两个数组，统计出每个物品两个维度的价值。这个题和前几个一样，价值 和重量一样，所以下面统称重量。

回想之前一维滚动数组的递推公式：dp[ j ]=max(dp[ j ], dp[ j - weight[ i ]] +value[ i ]);可见这个公式的重要性，所以还是根据这种思想，对于每个物品（每个k），都考虑没放进来之前的背包重量，是dp[ i- x ] [ j - y ]，放不进去的话就取上一轮的dp[i][j]。所以递推公式仍然是取这两种情况的最大值：

dp[ i ][ j ]=max( dp[ i ][ j ], dp[ i- x ] [ j - y ] + 1)。

注意这个是一维滚动数组的变形，但是因为dp数组扩展成二维，所以之前一维滚动数组的循环j这y一层循环应该变成两层循环i和j，加上最外层循环应该有3层for循环。

3. DP数组如何初始化。显然dp[0][0]是0，其他的值为了不会出现递推公式里面取max取到自己随便设置的一个正数，也应该都初始为0。

4. 遍历顺序。同样是先物品再背包，且背包有二维，i和j都应该倒序遍历，而且条件要使得递推公式的下标有效。

5. 打印DP数组。

以输入：["10","0001","111001","1","0"]，m = 3，n = 3为例

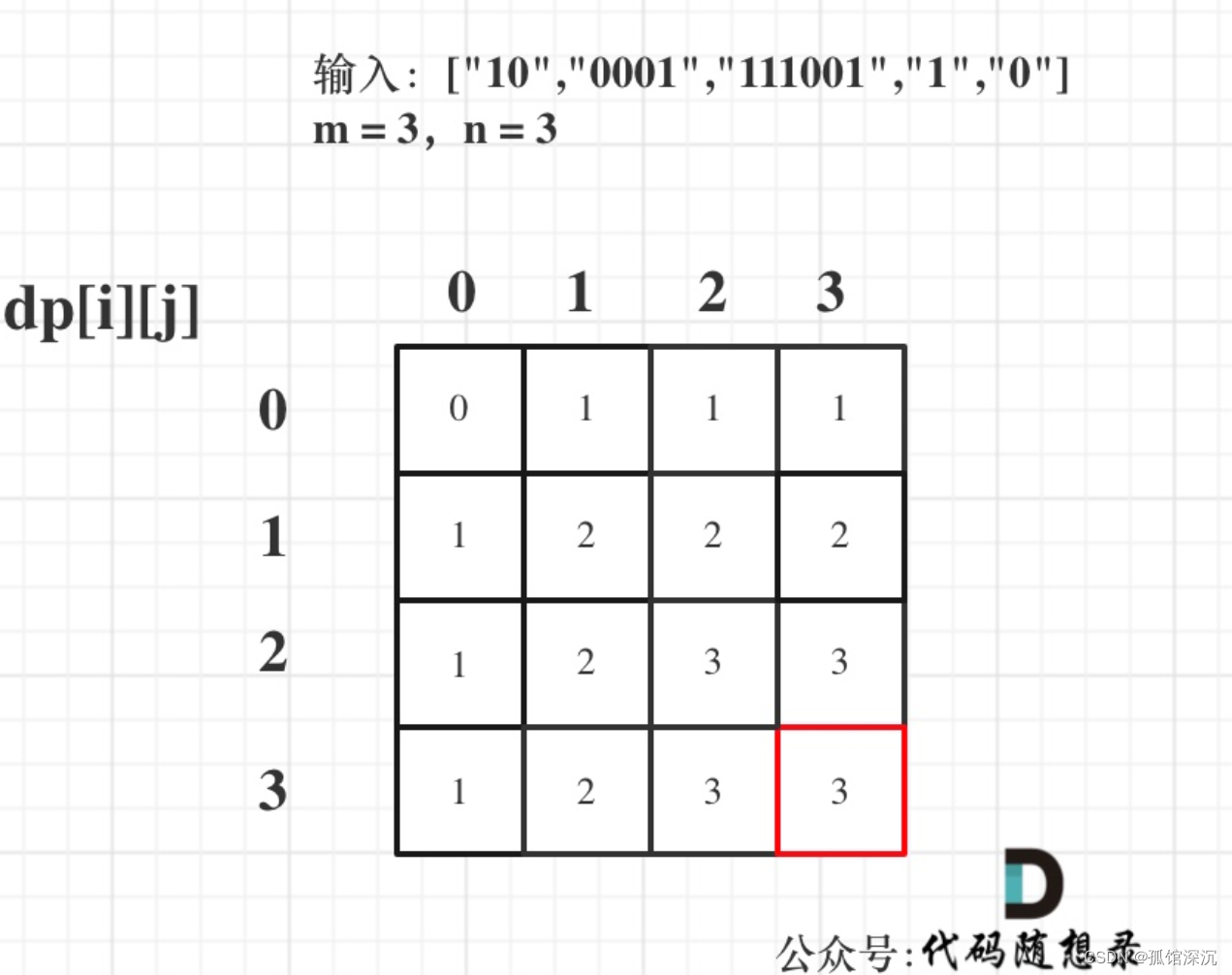
代码如下：

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1,0));    for(string str:strs){int x=0,y=0;//统计x和yfor(char s:str){if(s=='0')  x++;else y++;}//二维递推for(int i=m;i>=x;--i){for(int j=n;j>=y;--j){dp[i][j]=max(dp[i][j],dp[i-x][j-y]+1);}}}return dp[m][n];}
};