熵的最初来源于热力学。在热力学中,熵代表了系统的无序程度或混乱程度,也可以理解为系统的热力学状态的一种度量。后来被广泛引用于各个领域中,如信息学、统计学、AI等,甚至社会学当中。接下来将大家领略一下深度学习中熵的应用。
1. 熵(信息熵)
信息熵:Entropy,信息论中的概念,用来衡量信息的不确定性或随机性。信息熵越高,表示信息的不确定性越大。
1.1 自信息
自信息表示某一事件发生时所带来的信息量的多少,当事件发生的概率越大,则自信息越小。如何理解呢?如:某动物园猴子会说话这件事发生的概率很小,但是发生了,这一定是一个爆炸新闻,信息量很大,所以概率越小,信息量越大;相反,猴子不会说话,是一件确定的事情,概率很大,平平无奇的一件事,信息自然越小。公式可以用以下描述: P ( x i ) P(x_i) P(xi)表示随机变量 x i x_i xi发生的概率。 I ( P ( x i ) ) = − l o g ( P ( x i ) ) I(P(x_i)) = -log(P(x_i)) I(P(xi))=−log(P(xi))
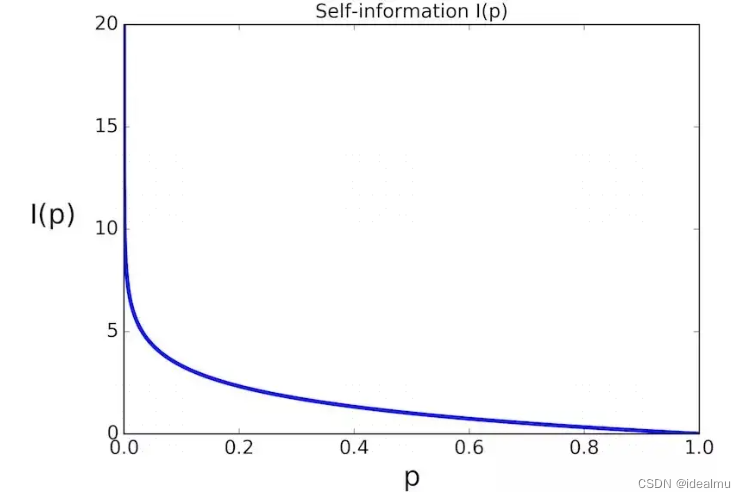
1.2 信息熵
自信息只能对单个事件信息描述,如果要对系统概率分布的平均信息量进行描述就需要信息熵,也就是所谓的熵。平均也就是求均值。
H ( X ) = E ( I ) = − E x ∼ P ( l o g ( P ( x i ) ) ) = − ∑ i = 1 n P ( x i ) l o g ( P ( x i ) ) H(X)=E(I)=-E_{x\sim P}(log(P(x_i)))=-\sum_{i=1}^nP(x_i)log(P(x_i)) H(X)=E(I)=−Ex∼P(log(P(xi)))=−i=1∑nP(xi)log(P(xi))
从公式可以看出,那些接近确定性的分布(输出几乎可以确定)具有较低的熵,那些接近均匀分布的概率分布具有较高的熵。如:二值分布,P(0) = 0 , P(1) = 1 带入公式得到 H=0。
2.交叉熵
2.1 交叉熵
交叉熵是一种用来衡量两个概率分布之间差异的指标,常用于评估模型输出与真实标签之间的差异。先看公式:
H ( P , Q ) = − E x ∼ P ∑ i = 1 n l o g ( Q ( x i ) ) = ∑ i = 1 n P ( x i ) l o g ( Q ( x i ) ) H(P,Q)=-E_{x\sim P}\sum_{i=1}^nlog(Q(x_i))=\sum_{i=1}^nP(x_i)log(Q(x_i)) H(P,Q)=−Ex∼Pi=1∑nlog(Q(xi))=i=1∑nP(xi)log(Q(xi))
P ( x i ) P(x_i) P(xi) 是真实分布, Q ( x i ) Q(x_i) Q(xi)是模型预测分布,假如模型预测分布等于真实分布,则 H ( P , Q ) = − ∑ i = 1 n P ( x i ) l o g ( P ( x i ) ) = H ( P ) H(P,Q)=-\sum_{i=1}^nP(x_i)log(P(x_i))=H(P) H(P,Q)=−∑i=1nP(xi)log(P(xi))=H(P),可以看出即使预测很准确,交叉熵也不等于0,但是为什么模型优化,对于分类任务使用交叉熵呢。将交叉熵公式变形得到:
H ( P , Q ) = − ∑ i = 1 n P ( x i ) l o g ( Q ( x i ) ) − ∑ i = 1 n P ( x i ) l o g ( P ( x i ) ) + ∑ i = 1 n P ( x i ) l o g ( P ( x i ) ) = − ∑ i = 1 n P ( x i ) l o g ( Q ( x i ) P ( x i ) ) + H ( P ) H(P,Q)=-\sum_{i=1}^nP(x_i)log(Q(x_i)) - \sum_{i=1}^nP(x_i)log(P(x_i)) + \sum_{i=1}^nP(x_i)log(P(x_i))\\=-\sum_{i=1}^nP(x_i)log(\frac{Q(x_i)}{P(x_i)}) + H(P) H(P,Q)=−i=1∑nP(xi)log(Q(xi))−i=1∑nP(xi)log(P(xi))+i=1∑nP(xi)log(P(xi))=−i=1∑nP(xi)log(P(xi)Q(xi))+H(P)
定义KL散度: D K L ( P ∣ ∣ Q ) = − ∑ i = 1 n P ( x i ) l o g ( Q ( x i ) P ( x i ) ) D_{KL}(P||Q) = -\sum_{i=1}^nP(x_i)log(\frac{Q(x_i)}{P(x_i)}) DKL(P∣∣Q)=−∑i=1nP(xi)log(P(xi)Q(xi)) ,所以 H ( P , Q ) = D K L ( P ∣ ∣ Q ) + H ( P ) H(P,Q)=D_{KL}(P||Q)+H(P) H(P,Q)=DKL(P∣∣Q)+H(P),由于P是真实值,其H(P )必然为固定值,因此对 H ( P , Q ) H(P,Q) H(P,Q)求梯度实际上是对 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)求梯度,因此在分类任务中交叉熵的优化任务可以看成是对 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)优化。
我们再看一下 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)公式,如果想要其最小,则势必Q(x)=P(x),因此优化交叉熵 H ( P , Q ) H(P,Q) H(P,Q)和优化KL散度 D K L ( P ∣ ∣ Q ) D_{KL}(P||Q) DKL(P∣∣Q)是一样的,从公式复杂程度来看,优化交叉熵会更简单一些,这也是为什么分类任务模型训练更喜欢用交叉熵损失,而这只是其中一个原因。我们可以接下来看,既然有了交叉熵,为什么还有KL散度,后面在介绍原因。
2.2 交叉熵损失
2.2.1 逻辑回归
我们先看一下最初的逻辑回归公式,有人说来源于最小化交叉熵,也有人说来源于最大释然估计,其实两种说法是等价的。2.1已经证明最小化交叉熵的结果是使预测值Q(x)=P(x),对于分类任务(逻辑回归)我们的目的也是如此,希望预测概率和真实概率一致。因此定义了预测概率函数 h θ ( x ) h_\theta(x) hθ(x)代替Q(x),真实值 y y y代替P(x),因此由交叉熵演变的二分类逻辑回归损失函数为,这里y=0或者1,因此二值的概率也可写为 h θ ( x ) , 1 − h θ ( x ) h_\theta(x),1 - h_\theta(x) hθ(x),1−hθ(x)
J ( θ ) = − ∑ i = 0 , 1 y l o g h θ ( x ) = y l o g h θ ( x ) + ( 1 − y ) l o g ( 1 − h θ ( x ) ) J(\theta)=-\sum_{i=0,1}ylogh_\theta(x) = ylogh_\theta(x) + (1-y)log(1-h_\theta(x)) J(θ)=−i=0,1∑yloghθ(x)=yloghθ(x)+(1−y)log(1−hθ(x))
这就是我们熟悉的二分类的逻辑回归损失了,如果是n分类呢,二分类只不过是多分类的一个特例,这里的 h θ ( x ) h_\theta(x) hθ(x)使用 q i q_i qi代替,
C r o s s E n t r o p y L o s s = J ( θ ) = − ∑ i = 1 n y i l o g ( q i ( x , θ ) ) CrossEntropy Loss = J(\theta)=-\sum_{i=1}^ny_ilog(q_i(x,\theta)) CrossEntropyLoss=J(θ)=−i=1∑nyilog(qi(x,θ))
q i ( x , θ ) q_i(x,\theta) qi(x,θ)是模型预测并且经过softmax的结果,n是类别数
2.2.2 交叉熵损失
2.1 说了交叉熵的优化结果不能使交叉熵的值为0,但是能够使预测值趋向真实值,也做了推导。而交叉熵损失函数在多分类优化结果是怎样的呢。我们想得到预测值跟真实值一样,过来一个样本,假如真实值标签是5,因此我们希望预测概率 q 5 ( x , θ ) = 1 q_5(x,\theta)=1 q5(x,θ)=1,其他为0,而我们损失函数必然为0,因此我们所用的交叉熵损失函数在分类任务最终理想结果是为0这不同于交叉熵,交叉熵一定会大于0。
为什么不用KL散度? 对于分类任务来说,真实值分布P(x),习惯上叫先验分布是难以确定的,比如说一张图片是猫是狗还是牛马,满足什么分布呢?很难说吧!而在生成模型中,KL散度却被广泛应用,原因是因为生成模型中假定了其分布为正态分布。后续有时间会写VQ-VAE一些生成模型,在介绍吧。
3.相对熵( KL散度)
公式: D K L ( P ∣ ∣ Q ) = − ∑ i = 1 n P ( x i ) l o g ( Q ( x i ) P ( x i ) ) D_{KL}(P||Q) = -\sum_{i=1}^nP(x_i)log(\frac{Q(x_i)}{P(x_i)}) DKL(P∣∣Q)=−∑i=1nP(xi)log(P(xi)Q(xi))
在2.1中已经隐藏的介绍了KL散度,这其实完全是用来衡量两个概率分布之间的相似性。KL=0,则完全表明Q(x)=P(x),预测值跟真实值一样。其在生成模型中应用较为广泛
4.极大释然估计
释然函数:
L ( θ ) = ∏ i = 0 n Q ( x i , θ ) L (\theta)= \prod_{i = 0}^{n}Q(x_i,\theta) L(θ)=i=0∏nQ(xi,θ)
优化释然函数,当所有随机变量概率相乘得到最大L时,此时的 θ \theta θ为最优解
等价于优化取对数最大值结果 l o g ( L ( θ ) ) = ∑ i = 0 n Q ( x i , θ ) log(L (\theta))= \sum_{i = 0}^{n}Q(x_i,\theta) log(L(θ))=∑i=0nQ(xi,θ),
等价于优化取相反数最小结果 − l o g ( L ( θ ) ) = − ∑ i = 0 n l o g ( Q ( x i , θ ) ) -log(L (\theta))=- \sum_{i = 0}^{n}log(Q(x_i,\theta)) −log(L(θ))=−∑i=0nlog(Q(xi,θ)),
等价于优化取均值最小结果 E ( . . . ) = − E x ∼ Q ∑ i = 0 n l o g ( Q ( x i , θ ) ) E(...)=- E_{x\sim Q}\sum_{i = 0}^{n}log(Q(x_i,\theta)) E(...)=−Ex∼Q∑i=0nlog(Q(xi,θ)),
由于Q分布最终预测是近似P分布,所以 E ( . . . ) ≈ E x ∼ P ∑ i = 0 n l o g ( Q ( x i , θ ) ) E(...)\approx E_{x\sim P}\sum_{i = 0}^{n}log(Q(x_i,\theta)) E(...)≈Ex∼P∑i=0nlog(Q(xi,θ)),
上式就是交叉熵的公式H(P,Q)。
因此最终我们得到以下结论:
优化极大释然函数=优化最小值交叉熵=优化最小值KL散度
5.备注参考说明
备注:文中所有真实分布为p或P,预测分布为q或Q。
参考:
https://zhuanlan.zhihu.com/p/35423404
https://blog.csdn.net/SongGu1996/article/details/99056721
https://zhuanlan.zhihu.com/p/38853901




![[Algorithm][前缀和][和为K的子数组][和可被K整除的子数组][连续数组][矩阵区域和]详细讲解](https://img-blog.csdnimg.cn/direct/62502bb9feed47ea98b3674669cc7d45.png)




![[Linux_IMX6ULL驱动开发]-设备树简述](https://img-blog.csdnimg.cn/direct/c85d70cf72ea4e5f90b939acfa039fb7.png)