深度学习入门之基于MLP的加州房价预测模型

       

  为了完成学校布置的课程任务并分享深度学习知识，写下了这篇文章，重点来分享一些建模任务中常用的技巧以及pytorch构建NN(神经网络)的基本方法，本次模型建立的数据源是加州房价数据集，这是一个较为经典的数据集：

一、数据预处理

数据读取

#依赖库和数据导入
import polars as pl#pl是一个基于Rust的数据处理库，速度比pandas快很多
import pandas as pd
def read_large_csv(file_path:str):"""使用polars读取大型csv文件Args:file_path:文件路径Returns:pandas类型的DataFrame"""reader = pl.read_csv(file_path)return reader.to_pandas()
data=read_large_csv(r'./housing/housing/housing.csv')
real_types=['NEAR BAY','INLAND','NEAR OCEAN']
print(f'ocean_proximity类型:{list(set(data["ocean_proximity"]))}')
print(f'其中为异常值的为{set(data["ocean_proximity"])-set(real_types)}')
print('\n')
print('数据预处理前:')
print(f'----------------------------------------------------------------------------')
print(f'数据大小:{data.shape}')
print(f'特征名称:{data.columns.tolist()}')

Housing.csv中共有以下特征:

longitude	经度
latitude	纬度
housing_median_age	住房平均年龄
total_rooms	房间总数
total_bedrooms	卧室总数
population	人口总数
households	住房户数
median_income	家庭收入中位数
median_house_value	房价中位数
ocean_proximity	临海类型

其中，数值类型的特征有housing_median_age,total_rooms,total_bedrooms,population

Households,median_income,median_house_value

异常值处理

            通过list(set())我们可以实现对列表去重,同时也可以用来查看某一列特征的所有取值

print(f'数据未处理前Ocean_proximity共有以下类型:{list(set(data['ocean_proximity']))')

           在所给数据ocean_proximity中,存在着一些异常数据，上方代码的输出结果为：

        数据未处理前Ocean_proximity:共有以下类型['NEAR OCEAN', 'NEAR BAY', 'INLAND', 'ISLAND', '<1H OCEAN']

        显然,ISLAND和1HOCEAN是错误的分类！我们需要将其剔除掉,剔除的方法很简单,

       通过dataframe内置的isin()函数来筛选ocean_proximity的取值在['NEAR OCEAN', 'NEAR BAY', 'INLAND']内的行，即：

real_types=['NEAR BAY','INLAND','NEAR OCEAN']
data=data[data['ocean_proximity'].isin(real_types)]#通过isin()来判断是否在real_types中

然后,我们分别输出剔除异常值前后的数据shape，其分别为(20640, 10) ，(11394, 10)，异常值竟然有9246行！ 

one-hot编码

        考虑到ocean_proximity这一特征的数据类型与其他类型格格不入,我们对其进行one-hot编码,这个使用pandas内置的get_dummies()函数即可实现，即：

data=pd.get_dummies(data,columns=['ocean_proximity'],prefix='ocean')#onehot编码

        Columns是指需要onehot编码的列名,data是原始数据,prefix是指经过one-hot编码后，新的三个特征的前缀，前缀是用来加在column列拆分后,新增的columns内取值种类个新特征的名称前。

        这里，ocean_proximity共有INLAND,NEAR BAY,NEAR OCEAN三类,那么经过get_dummies函数后,新的数据中ocean_proxiimity这一列消失,那么取而代之的是

 ocean_INLAND,ocean_NEAR BAY,ocean_NEAR OCEAN

这里的prefix就是指每个新特征前的ocean，倘若不加，那么这三个特征名称还是沿用原来取值

    新的三个特征都是bool型(0 or 1)取值为1还是0取决于其在原来特征中出现的位置，比如,原来ocean_proximity所有为INLAND的行,在ocean_INLAND这列特征中为1，其余位置全为0。

使用value_counts()函数来看一下新增的这几个特征的取值统计：

        正如我们前边所言,每一个特征的取值只有01，这里体现为True与False类型是int64，是为了与其他数值型数据类型对其,方便运算。

数据预处理完整代码及结果

#依赖库和数据导入
import polars as pl#pl是一个基于Rust的数据处理库，速度比pandas快很多
import pandas as pd
def read_large_csv(file_path:str):"""使用polars读取大型csv文件Args:file_path:文件路径Returns:pandas类型的DataFrame"""reader = pl.read_csv(file_path)return reader.to_pandas()
data=read_large_csv(r'./housing/housing/housing.csv')
real_types=['NEAR BAY','INLAND','NEAR OCEAN']
print(f'ocean_proximity类型:{list(set(data["ocean_proximity"]))}')
print(f'其中为异常值的为{set(data["ocean_proximity"])-set(real_types)}')
print('\n')
print('数据预处理前:')
print(f'----------------------------------------------------------------------------')
print(f'数据大小:{data.shape}')
print(f'特征名称:{data.columns.tolist()}')
print(f'----------------------------------------------------------------------------\n')
print('数据预处理后(剔除异常值,one-hot编码):')
print(f'----------------------------------------------------------------------------')
#数据预处理
data=data.dropna()#去掉缺失值
data['median_house_value']=data['median_house_value']/10000#房价除以10000，单位变化为万美元,画图方便
#ISLAND,<1H OCEAN都是异常值，需要去掉这些行
real_types=['NEAR BAY','INLAND','NEAR OCEAN']
data=data[data['ocean_proximity'].isin(real_types)]#通过isin()来判断是否在real_types中
data=pd.get_dummies(data,columns=['ocean_proximity'],prefix='ocean')#onehot编码
print(f'数据大小:{data.shape}')
print(f'特征名称:{data.columns.tolist()}')
print(f'----------------------------------------------------------------------------')

结果: 

二、数据可视化

分析

 图1数值类型数据分布直方图与箱型图

        观察图1不难发现，所有数值数据的分布直方图均表现为右偏趋势，且箱型图中也存在许多极端高值，特别是median_house_value（房价中位数）这一特征(最后一行)，其右偏趋势尤为明显。这种形态分布说明均值大于中位数，数据中大部分值都低于均值，只有少数几个极高值拉高了整体的平均水平，这意味着加州房价的分布不均，多数地区房价相对较低，而少数地区房价极高。

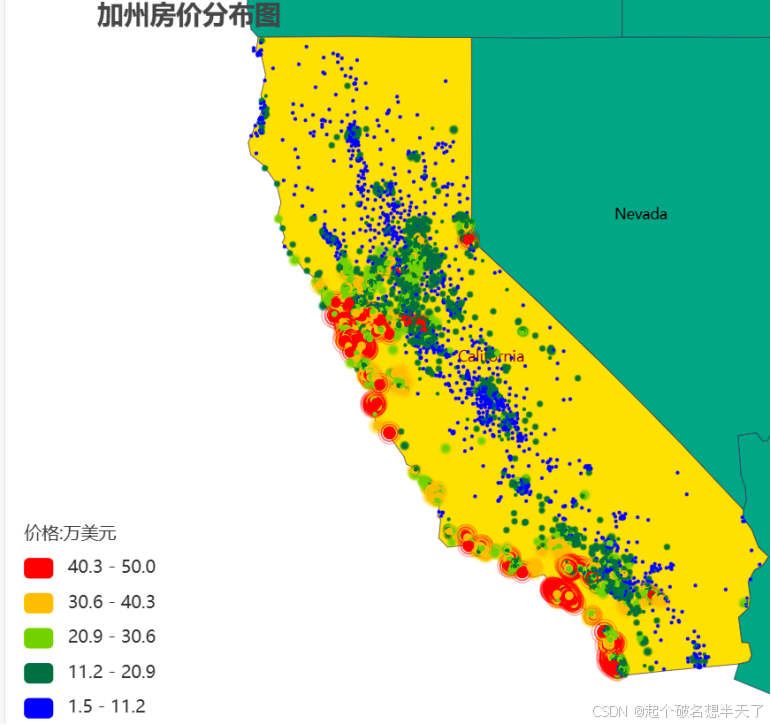
 图2加州房价地理分布

        图2所展示的加州房价分布散点图佐证了我们的这一猜想，价位较高的房屋抱团集中在NEAT BAY和NEAR OCEAN区域，而大部分内陆或偏远地区的房价则相对较低。 

图3 Inland,NearBay,NearOcean(从左至右)三区域房价分布箱型图 

        就图3而言，不难发现即使是Inland区域，也存在着不少房子价格水平与NearBay和NearOcean区域最高房价持平的地方，这些点在图3中的蓝色箱型图中体现为黑色离群点。 

        结合图1中所有区域的median_house_value的直方图与箱型图，可以得出结论：图三箱型图中的这些离群点正是导致直方图呈现极端右偏形态的罪魁祸首。

        这里我们并不把它们当做异常点，这是因为房价与身高年龄这些特征不一样,倘若这个箱型图描述的是人的身高分布，且黑色离群点的人的平均身高>2.5米，这就需要考虑剔除掉这些值了。

        但是房价是没有天花板的，房子的价格是取决于多种因素的,即使是地理区域不好的地方出现很高的房价也不难理解，当然，地理环境一定是这些因素中所占比重较大的那一个。

 结合网络查询,我找出了一些虽然深居内陆，但是房屋价格与海滨地区不相上下的区域如图4所示:

        总而言之，就房价均值来说,存在着明显的NearBay>=NearOcean>Inland的关系，这也很好理解,毕竟谁不想面朝大海,春暖花开呢？ 

可视化完整代码

数值型数据分布直方图与箱型图

#数据可视化
longitude=data['longitude']
latitude=data['latitude']
housing_median_age=data['housing_median_age']
total_rooms=data['total_rooms']
total_bedrooms=data['total_bedrooms']
population=data['population']
households=data['households']
median_income=data['median_income']
median_house_value=data['median_house_value']
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.suptitle('数据可视化')
plt.figure(figsize=(5,5),dpi=100)
plt.subplot(6,2,1),sns.histplot(total_rooms,kde=True),plt.xlabel('total_rooms')
plt.subplot(6,2,2),sns.boxplot(total_rooms,color='red'),plt.xlabel('total_rooms')
plt.subplot(6,2,3),sns.histplot(total_bedrooms,kde=True),plt.xlabel('total_bedrooms')
plt.subplot(6,2,4),sns.boxplot(total_bedrooms,color='red'),plt.xlabel('total_bedrooms')
plt.subplot(6,2,5),sns.histplot(population,kde=True),plt.xlabel('population')
plt.subplot(6,2,6),sns.boxplot(population,color='red'),plt.xlabel('population')
plt.subplot(6,2,7),sns.histplot(median_income,kde=True),plt.xlabel('median_income')
plt.subplot(6,2,8),sns.boxplot(median_income,color='red'),plt.xlabel('median_income')
plt.subplot(6,2,9),sns.histplot(households,kde=True),plt.xlabel('households')
plt.subplot(6,2,10),sns.boxplot(households,color='red'),plt.xlabel('households')
plt.subplot(6,2,11),sns.histplot(median_house_value,kde=True),plt.xlabel('median_house_value')
plt.subplot(6,2,12),sns.boxplot(median_house_value,color='red'),plt.xlabel('median_house_value')
plt.show()

 注意:data是运行完数据预处理完整代码后的结果。

INLAND NearBay NearOcean三区域房价箱型图：

#分别对编码后的不同ocean_proximity特征进行箱线图绘制
NearBay=data[data['ocean_NEAR BAY']==True]
Inland=data[data['ocean_INLAND']==True]
NearOcean=data[data['ocean_NEAR OCEAN']==True]
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.figure(figsize=(15,10))
plt.subplot(1,3,1),sns.boxplot(Inland['median_house_value'],color='blue')
plt.subplot(1,3,2),sns.boxplot(NearBay['median_house_value'],color='red')
plt.subplot(1,3,3),sns.boxplot(NearOcean['median_house_value'],color='green')
plt.show()

  注意:data是运行完数据预处理完整代码后的结果

加州房价分布地图：

nearbay=data[data['ocean_NEAR BAY']==True]#
inland=data[data['ocean_INLAND']==True]
nearocean=data[data['ocean_NEAR OCEAN']==True]
from pyecharts import options as opts
from pyecharts.charts import Geo
from pyecharts.globals import ChartType
map_data=pd.concat([nearbay,inland,nearocean],axis=0,ignore_index=True)
#使用pyecharts绘制加州地图
mapping_data= [(str(i)+'号小区',map_data['longitude'][i], map_data['latitude'][i], map_data['median_house_value'][i]) for i in range(map_data.shape[0])]
geo = Geo()
geo.add_schema(maptype="美国",  zoom=5,center=[-119.4179, 36.7783], #加利福尼亚的中心位置is_roam=True ,selected_mode=True,label_opts=opts.LabelOpts(font_size=10),itemstyle_opts=opts.ItemStyleOpts(color="#008f7a", border_color="#4b4453") #背景绿色,边界黑色
)
for name,lontitude,latitude,price in mapping_data:geo.add_coordinate(name,lontitude,latitude) #添加坐标geo.add("",[(name,price)],#房价单位转换成万type_=ChartType.EFFECT_SCATTER,symbol_size=price//6, #根据房价设置点的大小color="red"  #点的颜色)#设置地图配置
geo.set_global_opts(legend_opts=opts.LegendOpts(is_show=True),title_opts=opts.TitleOpts(title="加州房价分布图",pos_left=50),  # 标题visualmap_opts=opts.VisualMapOpts(is_piecewise=True,range_color=["blue", "green", "yellow", "red"],range_text=['价格:万美元'],min_=round(min(map_data["median_house_value"]),1),#最小房价max_=round(max(map_data["median_house_value"]),1)#最大房价)
)geo.render('加州房价分布图.html')

        注意:data是运行完数据预处理完整代码后的结果，运行上述代码后将会在当前工作文件夹下生成一个html文件,在浏览器中打开就可以得到我们前边图2所示的加州房价分布图了。

三、相关性分析 

在相关性分析这里，首先来计算一下各个特征之间的spearman相关系数，以及各个特征相对median_house_value的相关系数

Spearman相关系数被定义成等级变量之间的pearson相关系数。对于样本容量为n的样本，n个原始数据被转换成等级数据，相关系数ρ为

变量Xi	降序位置	等级xi
0.8	5	5
1.2	4	3.5
1.2	3	3.5
2.3	2	2
18	1	1

实际应用中，变量间的连结是无关紧要的，于是可以通过简单的步骤计算ρ.被观测的两个变量的等级的差值，以上述表格数据为参照，则ρ为

Spearman相关系数是在pearson相关系数的基础上考虑了数据分布的非线性关系，它衡量的是两个变量的排序之间的相关性，而不是它们之间的线性关系。

在pandas中,我们只需要调用corr()函数即可实现计算spearman相关系数：

#相关性分析
#计算每个特征相对于房价的spearman相关性系数
correlations=[]
names=[]
columns=data.columns.tolist()
columns=[column for column in columns if column!='median_house_value']
for column in columns:correlations.append(data[column].corr(data['median_house_value'],method='spearman'))names.append(column)
mapping_data={'names':columns,'correlations':correlations}
mapping_data=pd.DataFrame(mapping_data)
#计算每个特征相对于房价的spearman相关性系数
#计算sprarman相关性矩阵
corr_matrix=data.corr('spearman')
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
color_palette=['red','green','pink','purple','#ae5d00','#00d2fc','#3596b5','#cf3d2a','#00896f','#936c00','#4b4453']
plt.figure(figsize=(20,10),dpi=100)
plt.suptitle('相关性分析')
plt.subplot(1,2,1),sns.heatmap(corr_matrix,cmap='coolwarm',annot=True),plt.title('相关性矩阵')
plt.subplot(1,2,2),sns.barplot(data=mapping_data,y='names',x='correlations',width=0.5,hue='names',palette=color_palette),plt.text(x=max(correlations),y=len(names)*0.65,s='相关性最高'),plt.grid(),plt.title('各特征相对于房价的相关性')
plt.tight_layout()
plt.show()

结果:

        观察上图,我们不难发现对房价影响程度最高的是median_income人均收入这一特征,最低的是population人口数量这一特征,并且household，totalrooms，totalbedroom这几个变量之间自相关性比较高。考虑到模型精度,接下来对这几个特征进行提取与重构。 

四、特征提取构建

center_proximity

        在所给数据中，纬度与经度是两个地理参数，根据这两组参数来直接预测房价太过于勉强，解释意义不大，因此这里我们使用这两个原始特征构建一个新的特征，名为center_proximity

其计算公式如下：

        其中cp为center_proximity缩写,i表示第i个小区 ，,分别表示该小区的经纬度,

,则是指在InLand，NearBay，NearOcean这三个区域房价最高的小区的经纬度。那么实际上就是三个区域内每个小区距离其自身区域房价最高的小区的欧氏距离。

        所谓近朱者赤，近墨者黑，使用上述特征能够很好的衡量这一句话对房屋价格的影响。当然，这里我的地理水平有限。利用经纬度计算距离只是简单的将其当做坐标点计算欧式距离。如有更好的方法欢迎大佬指点。

average_room_num

data['average_room_num']=data['total_rooms']/data['households']#每个家庭的平均房间数

        这个特征表示每个家庭的平均房间数，一个拥有更多房间的家庭可能意味着更高的居住舒适度和更大的生活空间，房子价格也自然会高一些。

bedroom_raito

data['bedroom_ratio']=data['total_bedrooms']/data['households']#每个家庭的平均卧室数

这个特征表示卧室在总房间中的比例，可以反映住房的布局和设计。Bedroomratio高的房子说明该房子功能单一，只能满足日常居住需求，而Bedroomratio低的房子可能意味着房间功能多样，例如有书房、衣帽间、健身房等，更能满足现代人对居住品质的追求。价格也自然而然会更高一些。

population_per_households

data['population_per_households']=data['population']/data['households']

        这个特征表示每个家庭平均拥有的人口数量，人口数量多的家庭,可以反映家庭的结构和规模。通常情况下，每个家庭平均人口数量较少的房子，可能意味着家庭成员较少，房子价格可能会相对高一些。这是因为家庭成员少的家庭往往更加注重生活品质和个人空间，对房子的装修、设计和周边环境会有更高的要求。相反，家庭成员多的家庭可能更注重实用性，对价格更为敏感。

        最后，不要忘了删除掉原来的一些特征：

data.drop(['population','total_rooms','total_bedrooms'],axis=1,inplace=True)

        特征重构后的相关性系数矩阵热力图及各特征相对房屋价格相关系数柱状图

        经过特征提取与重构后,各个特征间的互相关性不再那么明显,且提取到的新特征相对median_house_value的相关性也比原来更高。

五、MLP模型         

模型设定：

epoches	300
Batch_size	10
Activate function	Relu
hiddenlayer_num	2
inputsize	128,64
outputsize	1

完整代码:

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
df=data.copy()
target='median_house_value'
features=df.drop(target, axis=1).columns.tolist()
print(f'参与训练的特征有:{features}')
X = df[features].values
y = df[target].values.reshape(-1, 1)#划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42
)#标准化
scaler_X = StandardScaler()
X_train_scaled = scaler_X.fit_transform(X_train)
X_test_scaled = scaler_X.transform(X_test)
scaler_y = StandardScaler()
y_train_scaled=scaler_y.fit_transform(y_train)
y_test_scaled=scaler_y.transform(y_test)# 转换为tensor
X_train_tensor=torch.tensor(X_train_scaled, dtype=torch.float32)
X_test_tensor=torch.tensor(X_test_scaled, dtype=torch.float32)
y_train_tensor=torch.tensor(y_train_scaled, dtype=torch.float32)
y_test_tensor=torch.tensor(y_test_scaled, dtype=torch.float32)# 定义 MLP 模型
class MLP(nn.Module):def __init__(self, input_size, hidden_sizes, output_size):super(MLP, self).__init__()layers=[]in_size=input_sizefor hidden_size in hidden_sizes:layers.append(nn.Linear(in_size, hidden_size))layers.append(nn.ReLU())in_size = hidden_sizelayers.append(nn.Linear(in_size, output_size))self.network=nn.Sequential(*layers)def forward(self, x):return self.network(x)# 初始化模型参数
input_size=X_train_tensor.shape[1]
hidden_sizes=[128, 64]#隐藏层和神经元数量
output_size=1 #预测的是单个值model=MLP(input_size, hidden_sizes, output_size)# 损失函数MSE和优化器Adam
criterion=nn.MSELoss()
optimizer=optim.Adam(model.parameters(), lr=0.008)# 训练模型并记录损失
num_epochs=300
train_losses=[]
test_losses=[]
for epoch in range(num_epochs):# 训练模式model.train()optimizer.zero_grad()#前向传播outputs=model(X_train_tensor)loss=criterion(outputs, y_train_tensor)#反向传播和优化loss.backward()optimizer.step()train_losses.append(loss.item())# 评估模式model.eval()with torch.no_grad():test_outputs = model(X_test_tensor)test_loss = criterion(test_outputs, y_test_tensor)test_losses.append(test_loss.item())if (epoch+1) % 20 == 0:print(f'Epoch [{epoch+1}/{num_epochs}], Train Loss: {loss.item():.6f}, Test Loss: {test_loss.item():.6f}')# 绘制训练和测试误差变化曲线
plt.figure(figsize=(10, 5))
plt.plot(range(1, num_epochs+1), train_losses, label='Train Loss (MSE)')
plt.plot(range(1, num_epochs+1), test_losses, label='Test Loss (MSE)')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('每轮训练集与测试集损失')
plt.legend()
plt.grid(True)
plt.show()# 进行最终预测
model.eval()
with torch.no_grad():y_pred_scaled = model(X_test_tensor).numpy()
# 反缩放预测值和真实值
y_pred = scaler_y.inverse_transform(y_pred_scaled)[:200]
y_test_actual = scaler_y.inverse_transform(y_test_tensor.numpy())[:200]
# 绘制实际价格与预测价格的折线图
plt.figure(figsize=(12, 6))
plt.plot(y_test_actual, label='实际价格', color='blue')
plt.plot(y_pred, label='预测价格', color='red', alpha=0.7)
plt.xlabel('预测样本数量索引')
plt.ylabel('房价')
plt.title('实际房价Vs预测房价(折线图)')
plt.legend()
plt.grid(True)
plt.show()
# 绘制实际价格与预测价格的散点图
plt.figure(figsize=(8, 8))
plt.scatter(y_test_actual, y_pred, alpha=0.5)
plt.plot([y_test_actual.min(), y_test_actual.max()], [y_test_actual.min(), y_test_actual.max()], 'r--', lw=2, label='Ideal Fit')
plt.xlabel('真实房价')
plt.ylabel('预测房价')
plt.title('真实房价Vs预测房价(散点图)')
plt.legend()
plt.grid(True)
plt.show()

模型评估 

 原始数据结果vs特征提取结果:

 

只看上边这两个图不明显,我们看一看散点图 ：

         理想的预测结果是，所有的散点都密集地均匀集中分布在红线两侧，下方这个图是经过特征工程后的预测结果,对比上下两个图不难发现,下方的图像整体上散点更集中，分布更加均匀，说明经过特征工程后的模型预测结果更加稳定，误差也更小。从图中可以直观地看到，经过特征工程后的模型对房价的预测更加准确，能够更好地捕捉到数据中的规律。 这也验证了特征工程在深度学习中的重要性，通过对原始数据进行合理的处理和转换，可以显著提高模型的性能和预测效果。正所谓数据是模型的粮食

总结

 

        以上便是基于MLP的加州房价预测模型的所有内容，后续我还将分享更多深度学习实战案例，感谢大家支持！