数据结构之堆的实现以及性质和应用
上篇文章(数据结构之堆和二叉树的简介-CSDN博客)介绍了什么是二叉树以及堆的概念,在这篇文章中我们将进一步实现堆及其应用
1. 实现顺序结构二叉树
⼀般堆使用顺序结构的数组来存储数据,堆是⼀种特殊的⼆叉树,具有⼆叉树的特性的同时,还具备其他的特性。
1.1 堆的概念与结构
如果有⼀个关键码的集合 ,把它的所有元素按完全⼆叉树的顺序存储方式存储,在⼀个⼀维数组中,并满足: 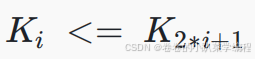

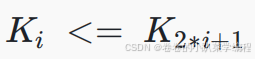

i = 0 、 1 、 2... ,则称为小堆(或大堆)。将根结点最大的堆叫做最⼤堆或⼤根堆,根结点最⼩的堆
叫做最小堆或小根堆。

💡 ⼆叉树性质
• 对于具有 n 个结点的完全⼆叉树,如果按照从上⾄下从左⾄右的数组顺序对所有结点从
0 开始编号,则对于序号为 i 的结点有:
1. 若 i>0 , i 位置结点的双亲序号: (i-1)/2 ; i=0 , i 为根结点编号,⽆双亲结点
2. 若 2i+1<n ,左孩⼦序号: 2i+1 , 2i+1>=n 否则无左孩子
3. 若 2i+2<n ,右孩⼦序号: 2i+2 , 2i+2>=n 否则无右孩子
1.2 堆的实现及一些基本操作
我们还是定义三个文件
这是heap.h文件
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>typedef int hpdatatype;
//堆的结构
typedef struct heap
{hpdatatype* arr;int size; //有效数据个数int capacity; //容量
}hp;
void hpinit(hp* php);
void hpdestroy(hp* php);
void hppush(hp* php, hpdatatype x); //插入数据
void hppop(hp* php); //删除堆顶数据
bool hpempty(hp* php); //判空
int hpsize(hp* php); //求size
hpdatatype hptop(hp* php); //获取堆顶元素
void swap(int* x, int* y);
void adjustdown(hpdatatype* arr, int parent, int n);
void adjustup(hpdatatype* arr, int child);这是heap.c文件
#include"heap.h"
void hpinit(hp* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;
}
void hpdestroy(hp* php)
{if (php->arr){free(php->arr);}php->arr = NULL;php->capacity = php->size = 0;
}
void swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
void adjustup(hpdatatype* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){//> : 大堆//< : 小堆if (arr[child] < arr[parent]){swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void adjustdown(hpdatatype* arr, int parent, int n)
{int child = parent * 2 + 1;while (child < n){//先找小的孩子if (child + 1 < n && arr[child] > arr[child + 1]) //要保证右孩子也没出界{child++;}//将小孩子与父节点比较if (arr[child] < arr[parent]){swap(&arr[child], &arr[parent]); //此时值交换完了,下表还没变parent = child;child = parent * 2 + 1;}else{break;}}
}
void hppush(hp* php, hpdatatype x)
{assert(php);//既然要插入,就要判断容量够不够if (php->capacity == php->size){int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;hpdatatype* tmp = (hpdatatype*)realloc(php->arr,sizeof(hpdatatype) * newcapacity);assert(tmp);php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size] = x; //先不管是大堆还是小堆,先把数插进去//向上调整adjustup(php->arr, php->size); //不断的让子节点和父节点比较,php->size指的是刚插入数据的下标php->size++;
}
bool hpempty(hp* php)
{assert(php);return php->size == 0;
}
int hpsize(hp* php)
{assert(php);return php->size;
}
//删除堆顶元素
void hppop(hp* php)
{assert(!hpempty(php));//先将堆顶元素与最后一个元素调换,便于将其删去,之后重新调整堆的结构swap(&php->arr[0], &php->arr[php->size - 1]);php->size--; //此时堆顶元素已经被删了,下一步就是按照大堆或者小堆的方式重新调整堆的结构adjustdown(php->arr,0, php->size);
}
//获取堆顶数据
hpdatatype hptop(hp* php)
{assert(!hpempty(php));return php->arr[0];
}
这是test.c文件
#include"heap.h"
void test()
{hp hp;hpinit(&hp);hppush(&hp, 1);hppush(&hp, 2);hppush(&hp, 3);hppush(&hp, 4);//while (!hpempty(&hp))//{// printf("%d", hptop(&hp));// hppop(&hp);//}hppop(&hp); //此时会发生assertion报错,原因是hppop函数中的assert函数报错,我们断言的 是不为空,但是上述打印过程已经让我们的堆变为空了hppop(&hp);while (!hpempty(&hp)){printf("%d", hptop(&hp));hppop(&hp);}hpdestroy(&hp);
}
int main()
{test();return 0;
}1.3数组的冒泡排序
这里仅展示关键代码,上述涉及的方法将不在赘述,以下内容均在test.c中实现
//时间复杂度O(N*2)
void bubblesort(int* arr, int n)
{for (int i= 0; i < n; i++){int exchange = 0;for (int j = 0; j < n - 1 - i; j++){if (arr[j] > arr[j + 1]){exchange = 1;swap(&arr[j], &arr[j + 1]);}}if (exchange == 0){break;}}
}
int main()
{进行冒泡排序(方法1)int arr1[] = { 17,20,10,13,19,15 };int n1 = sizeof(arr1) / sizeof(arr1[0]);bubblesort(arr1, n1);for (int i = 0; i < n1; i++){printf("%d ", arr1[i]);}printf("\n");//进行冒泡排序(方法2:利用堆的性质)int arr2[] = { 17,20,10,13,19,15 };int n2 = sizeof(arr2) / sizeof(arr2[0]);hp hp;hpinit(&hp);//调用push将数组中的数据建堆for (int i = 0; i < n2; i++){hppush(&hp, arr2[i]);}int i = 0;while (!hpempty(&hp)){arr2[i++] = hptop(&hp);hppop(&hp);}for (int i = 0; i < n2; i++){printf("%d ", arr2[i]);}hpdestroy(&hp);return 0;
}但是,真正的堆排序不是这种写法,堆排序是借助堆的算法思想,而不能够直接使用堆的数据结构来辅助实现!
1.4堆排序
这里仅展示关键代码,上述涉及的方法将不在赘述,以下内容均在test.c中实现
void heapsort(int* arr, int n)
{//根据给定的arr来进行建堆//child:n-1 parent:(child-1)/2=(n-2)/2//向下调整算法建堆//数组传过来的时候,堆就已经建好了,只不过是乱七八糟的,我们需要将其调整为大堆或者小堆for (int i = (n - 1 - 1) / 2; i >= 0; i--) //从根节点开始调整(对父节点下手){adjustdown(arr, i, n);}//堆排序int end = n - 1;while (end > 0){swap(&arr[0], &arr[end]);adjustdown(arr, 0, end);end--;}
}
int main()
{int arr3[] = { 17,20,10,13,19,15 };int n3 = sizeof(arr3) / sizeof(arr3[0]);heapsort(arr3, n3);for (int i = 0; i < n3; i++){printf("%d ", arr3[i]);}
return 0;
}由此,我们得出结论:排升序,建大堆,因为要把最大的元素与最后一个元素交换
排降序,建小堆,因为要把最小的元素与最后一个元素交换
注意:一开始建堆只是弄成了整体趋势由大到小的降序曲线,二次排序才是真正的排成了一个不 严谨(包括等于)的降序数组!
1.5topk问题
找最大的前k个数据,建小堆,比堆顶数据,谁大谁入堆
找最小的前k个数据,建大堆,比堆顶数据,谁小谁入堆
#define _CRT_SECURE_NO_WARNINGS 1
#include"heap.h"
#include <time.h>
void CreateNDate() {// 造数据 int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 1000000;fprintf(fin, "%d\n", x);}fprintf(fin, "%d\n", 2000000001);fprintf(fin, "%d\n", 2002323001);fprintf(fin, "%d\n", 2002323201);fprintf(fin, "%d\n", 2011110001);fprintf(fin, "%d\n", 2022220001);fclose(fin);
}
void topk()
{int k = 0;printf("input k:");scanf_s("%d", &k);const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen error");exit(1);}//找最大的前k个数,建小堆int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail!");exit(2);}//读取文件中前k个数据建堆for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);}//建堆for (int i = (k - 1 - 1) / 2; i > 0; i--){adjustdown(minheap, i, k);}//遍历剩下的n-k个数据,跟堆顶比较,谁大谁入堆//调整堆int x = 0;while (fscanf(fout, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x; //先把这个数据插进去,等下在调整adjustdown(minheap, 0, k);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}fclose(fout);
}
int main()
{CreateNDate();topk();return 0;
}