java算法OJ(4)树与二叉树
目录
编辑
1.前言
2.正文
2.1树的结构定义
2.2定义树的节点
2.3树的遍历
2.4递归实现
2.4.1树的前序遍历
2.4.1.1题目
2.4.1.2示例
2.4.1.3代码
2.4.2树的中序遍历
2.4.1.1题目
2.4.1.2示例
2.4.1.3代码
2.4.3树的后序遍历
2.4.1.1题目
2.4.1.2示例
2.4.1.3代码
2.4.4树的层序遍历
2.4.1.1题目
2.4.1.2示例
2.4.1.3代码
2.5非递归实现
3.小结
1.前言
哈喽大家好喔,今天博主继续进行数据结构的分享与学习,今天的主要内容是树与二叉树,从这节课开始就标志着数据结构从线性的转化为树形,让我们开始吧。
2.正文
2.1树的结构定义
我们如何来理解树的结构定义呢。让我们先看图片中的左侧一部分,1->4->6,是不是可以把它理解成为一个链表,那么链表中的next变量就是树的边界。那我们又如何实现其中一个节点可以往下指多个节点呢,即将类里面访问成员变量左右子树即可。

以下是树的结构特点:
- 有且仅有一个特定的节点被称为根节点(Root):树中的每个节点都直接或间接地与根节点相连。
- 树中的其他节点可以被分为m(m>0)个子树:这些子树本身也是树结构。
- 树中的节点不包含任何循环:即从任一节点出发,沿着有向边走,不能回到原节点。
2.2定义树的节点
讲完了树的结构定义,那么他到底代码是如何实现的呢,让我们逐层来分析:
首先需要一个头结点,既然是树那么就有俩个子节点,另外头节点和俩个子节点下都有需要存储的值,最后再在类里面写上构造方法,这个类就完成了。明白了我们所有需要的量,接下来就可以开始敲代码了。
public static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int v) {val = v;}}2.3树的遍历
在树中,一共有四种遍历的方式,前序遍历,中序遍历,后序遍历和层序遍历,接下来让我们详细讲解一下其中的含义:
前序遍历:
在前序遍历中,我们首先访问根节点,然后递归地对左子树进行前序遍历,最后递归地对右子树进行前序遍历。
访问顺序:根 -> 左 -> 右。
中序遍历:
在中序遍历中,我们首先递归地对左子树进行中序遍历,然后访问根节点,最后递归地对右子树进行中序遍历。
访问顺序:左 -> 根 -> 右。
中序遍历的一个重要特性是,它可以按照升序输出二叉搜索树中的所有节点。
后序遍历:
在后序遍历中,我们首先递归地对左子树进行后序遍历,然后递归地对右子树进行后序遍历,最后访问根节点。
访问顺序:左 -> 右 -> 根。
后序遍历通常用于删除二叉树,因为它可以确保在访问节点之前,其子节点已经被处理。
层序遍历:
通常使用队列来实现层序遍历,每次从队列中取出一个节点,访问它,然后将它的子节点加入队列中。
访问顺序:从树的顶部开始,逐层向下,每层从左到右访问所有节点。
2.4递归实现
下面四种遍历都主要的采用递归来进行实现,代码量不大但需要一定的理解,接下来我会详细的展开。
2.4.1树的前序遍历
144. 二叉树的前序遍历 - 力扣(LeetCode)
2.4.1.1题目

2.4.1.2示例

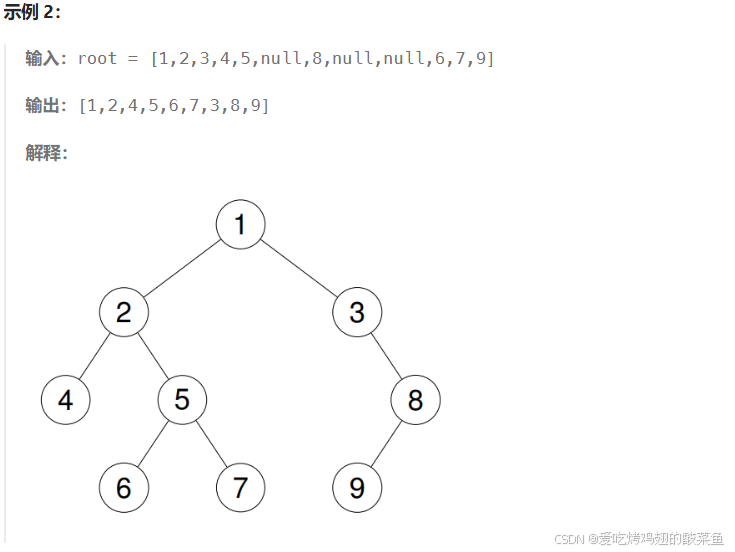

2.4.1.3代码
先看解析:
- 首先创造一个用于接受答案的列表
- 建立递归函数
- 如果递归函数是空则返回到上一步,非空而往下进行
- 先将中节点接入列表,先走左子树,左子树走完再走右子树,完成递归
- 最后return即可
下文的中序遍历和后序遍历只是代码逻辑顺序不同,实现思路一致,不做讲解。
再上代码:
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();preorder(root,res);return res;}public void preorder(TreeNode root,List<Integer>res){if(root == null)return ;res.add(root.val);preorder(root.left,res);preorder(root.right,res);}
}2.4.2树的中序遍历
94. 二叉树的中序遍历 - 力扣(LeetCode)
2.4.1.1题目

2.4.1.2示例

2.4.1.3代码
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();postorder(root,res);return res;}public void postorder(TreeNode root,List<Integer> res){if(root == null)return;postorder(root.left,res);res.add(root.val);postorder(root.right,res);}
}2.4.3树的后序遍历
145. 二叉树的后序遍历 - 力扣(LeetCode)
2.4.1.1题目

2.4.1.2示例



2.4.1.3代码
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();postorder(root,res);return res;}public void postorder(TreeNode root,List<Integer> res){if(root == null)return;postorder(root.left,res);postorder(root.right,res);res.add(root.val);}
}2.4.4树的层序遍历
102. 二叉树的层序遍历 - 力扣(LeetCode)
2.4.1.1题目

2.4.1.2示例

2.4.1.3代码
层序遍历需要稍微复杂一些,但是实现的方式也有很多,下面展示了其中的一种方式,有兴趣的小伙伴还可以尝试多种实现哦,上思路:
这道题主体思路就是先创建一个储存元素为列表的列表(题目要求的返回形式),用队列来模拟每一层的状态。
- 先将头节点压入队列,进入while循环,创建一个储存当前层的列表。
- 判断队列中元素数量作为for循环条件
- 先将队列中当前头节点元素压入储存当前层的列表,再将头节点弹出队列
- 如果左子树不为空,就把它压入队列,右节点同理
- 最后将本层列表压入res总列表中,继续下一次循环
- 此时原先的左右节点化为上文的头结点继续循环,直到二者皆为空。
- 最后return即可
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> res = new ArrayList<List<Integer>>();if(root == null)return res;Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);while(!queue.isEmpty()){LinkedList list = new LinkedList<Integer>();int n = queue.size();TreeNode treeNode = new TreeNode();for(int i = 0;i < n;i++){treeNode = queue.poll();list.add(treeNode.val);if(treeNode.left != null){queue.offer(treeNode.left);}if(treeNode.right != null){queue.offer(treeNode.right);}}res.add(list);}return res;}
}2.5非递归实现
当然除了通过递归实现树的各种遍历以外,还可以通过非递归的方式来进行实现,比如通过栈实现,下面我就以一个栈来实现后序遍历。
我们都知道后序遍历先打印左,再打印右,再打印中,栈是一种先进后出的数据结构,这样我们在把元素压入栈的时候则需要额外注意。过程如下:
- 先将头节点压入栈中
- 判断左子树是否为空或者是否被处理过,如果不为空也没被处理过则将其也压入栈中
- 右子树同上面理
- 如果遇到子书遍历到树底(即其左右子树均为空且该未被处理),打印后弹出
- 最后return即可
接下来我们附上代码:
public static void posOrderOneStack(TreeNode h) {if (h != null) {Stack<TreeNode> stack = new Stack<>();stack.push(h);while (!stack.isEmpty()) {TreeNode cur = stack.peek();if (cur.left != null && h != cur.left && h != cur.right) {stack.push(cur.left);} else if (cur.right != null && h != cur.right) {stack.push(cur.right);} else {System.out.print(cur.val + " ");h = stack.pop();} }System.out.println();}}3.小结
今天java算法OJ(4)树与二叉树到这里就结束了,不要忘了点一手关注再走哦,希望喜欢的朋友多多支持我哦~

