谈Sobel算子的数学推导——原来是四个方向的相加
An Isotropic 3x3 Image Gradient Operator
看了Sobel算子的作者Irwin Sobel解释Sobel算子的推导,才知道Sobel算子中的系数不是拍脑袋想的。

原文表述的不清晰,我这里对原文做解释。
本质是四个方向一阶中心差分的相加, h h h为街区距离。
目录
- 基础知识
- 一阶中心差分
- 街区距离
- 梯度
- Sobel的推导
- 四个方向的一阶中心差分
基础知识
一阶中心差分
对于一个函数 f ( x ) f(x) f(x),在点 x x x 处的一阶中心差分可以表示为:
f ′ ( x ) ≈ f ( x + h ) − f ( x − h ) 2 h f'(x) \approx \frac{f(x + h) - f(x - h)}{2h} f′(x)≈2hf(x+h)−f(x−h)
其中, h h h 是一个小的正数,表示步长。
街区距离

梯度
原文是笛卡尔坐标系,我这里用图像坐标系。

首先是梯度的定义,一阶导数有方向,函数值增加最快的方向。


把它理解为考虑两个方向的相加,向量相加符合:
三角形法则:将一个向量的尾部连接到另一个向量的头部,结果向量是从第一个向量的起点指向最后一个向量的终点的向量。
平行四边形法则:当两个向量从同一点出发时,以这两个向量为邻边构造一个平行四边形,结果向量就是从起点指向对角线另一端的向量。
设 f ( x , y ) f(x,y) f(x,y) 是一个二维离散函数,
∇ f ( x , y ) ≈ f ( x + 1 , y ) − f ( x − 1 , y ) 2 [ 1 0 ] + f ( x , y + 1 ) − f ( x , y − 1 ) 2 [ 0 1 ] \begin{aligned} \nabla f(x,y) \approx &\frac{f(x+1,y) - f(x-1,y)}{2} \begin{bmatrix} 1 \\0 \end {bmatrix} \\ &+ \frac{f(x,y+1) - f(x,y-1)}{2} \begin{bmatrix} 0 \\1 \end {bmatrix} \\ \end{aligned} ∇f(x,y)≈2f(x+1,y)−f(x−1,y)[10]+2f(x,y+1)−f(x,y−1)[01]
Sobel的推导
使用四个方向上的差分的求和作为二维离散函数梯度的估计。
“Numerical analysis teaches us that for certain classes of surfaces an even better
estimate is obtained using a weighted average of three such central differences … These
expressions produce excellent estimates for the components of the gradient of the central point”.
四个方向的一阶中心差分
街区距离中, x x x方向和 y y y方向 h = 1 h=1 h=1, x y xy xy方向和 − x y -xy −xy方向 h = 2 h=2 h=2。
- x x x方向: f ( x + 1 , y ) − f ( x − 1 , y ) 2 \frac{f(x+1,y)-f(x-1,y)}{2} 2f(x+1,y)−f(x−1,y)
- y y y方向: f ( x , y + 1 ) − f ( x , y − 1 ) 2 \frac{f(x,y+1)-f(x,y-1)}{2} 2f(x,y+1)−f(x,y−1)
- x y xy xy方向: f ( x + 1 , y + 1 ) − f ( x − 1 , y − 1 ) 4 \frac{f(x+1,y+1)-f(x-1,y-1)}{4} 4f(x+1,y+1)−f(x−1,y−1)
- − x y -xy −xy方向: f ( x − 1 , y + 1 ) − f ( x + 1 , y − 1 ) 4 \frac{f(x-1,y+1)-f(x+1,y-1)}{4} 4f(x−1,y+1)−f(x+1,y−1)
设 f ( x , y ) f(x,y) f(x,y) 是一个二维离散函数,它的梯度可以由4个方向相加进行估计:
∇ f ( x , y ) ≈ f ( x + 1 , y ) − f ( x − 1 , y ) 2 [ 1 0 ] + f ( x , y + 1 ) − f ( x , y − 1 ) 2 [ 0 1 ] + f ( x + 1 , y + 1 ) − f ( x − 1 , y − 1 ) 4 [ 1 1 ] + f ( x − 1 , y + 1 ) − f ( x + 1 , y − 1 ) 4 [ − 1 1 ] \begin{aligned} \nabla f(x,y) \approx &\frac{f(x+1,y) - f(x-1,y)}{2} \begin{bmatrix} 1 \\0 \end {bmatrix} \\ &+ \frac{f(x,y+1) - f(x,y-1)}{2} \begin{bmatrix} 0 \\1 \end {bmatrix} \\ &+ \frac{f(x+1,y+1) - f(x-1,y-1)}{4} \begin{bmatrix} 1 \\1 \end {bmatrix} \\ & + \frac{f(x-1,y+1) - f(x+1,y-1)}{4} \begin{bmatrix} -1 \\1 \end {bmatrix} \end{aligned} ∇f(x,y)≈2f(x+1,y)−f(x−1,y)[10]+2f(x,y+1)−f(x,y−1)[01]+4f(x+1,y+1)−f(x−1,y−1)[11]+4f(x−1,y+1)−f(x+1,y−1)[−11]
整理出 x x x 和 y y y 两个方向。

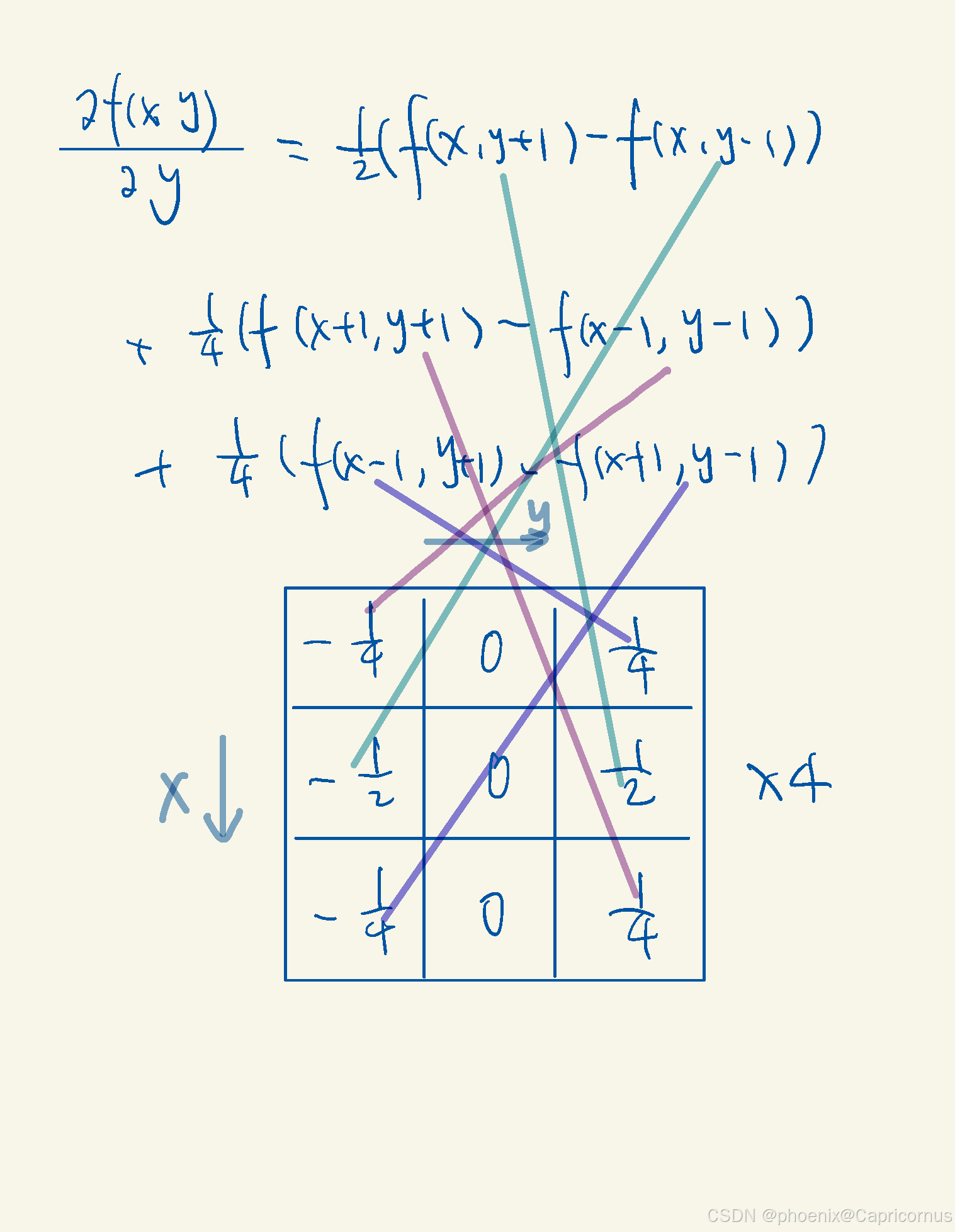
本应该除以4做平均,但是尺度不重要,那个时候计算能力不行,为了是整数,乘以4,就成了开篇的Sobel模板。实际是平均值的16倍。
一阶差分有方向,二阶差分没方向,拉普拉斯的原理和这个原理异曲同工。
冈萨雷斯的解释是加权平滑,这不是2的目的,但是可以做个解释。


