图的应用——最短路径
1.Dijkstra算法【单源最短路径】
1.1 步骤:
Dijkstra算法是一种用于求解加权图中单源最短路径问题的经典算法。其目的是从给定的源点到图中每个顶点的最短路径。其使用的是贪心策略,以下是Dijkstra算法的步骤:
1.初始化:
我们从起点(0号顶点)出发,也就是从0开始走。
一开始,把0号顶点放到集合S里,这个集合S表示“已经确定了最短路径的顶点”。初始化的时候,记录每个顶点到起点的距离(dist),起点到自己的距离就是0,其他顶点的距离先设置为从0号顶点到它的路径长度。如果没有直接的路径,就设置为“无穷大”(表示暂时还不知道怎么到达那里)。
2.选点:
从剩下没有加入S集合的顶点里,挑一个“距离最短”的顶点。也就是在当前所有已知路径里,找一个从起点出发,走最短路可以到达的下一个顶点。
一旦确定这个顶点,就把它加入集合S。
3.更新距离:
假设我们刚刚把某个顶点加入了集合S,现在我们看看:从这个顶点出发,能不能走到还没加入S的其他顶点。如果能走,而且这条路比之前知道的路径更短,就更新这些顶点的最短距离。
4.重复步骤2和3:
这个过程一直重复,直到所有的顶点都加入集合S,也就是说起点到所有其他顶点的最短路径都找到了。
每次你都会更新一下已知的最短路径,直到所有点的最短路径都确定了。这就是Dijkstra算法的核心思想——不断找出当前的最短路径,然后更新和修正它。
1.2 示例:
求一个点(a)到其他点之间的最短路径,每次选距离a最近的点,然后更新。
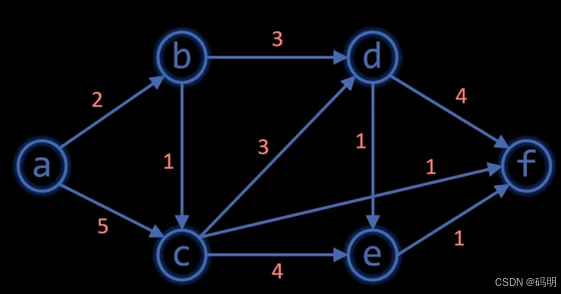
填写距离,到达不了的写∞
步骤 1:
选择距离最小的节点 a(初始时为0),更新其邻接节点 b 和 c 的距离:
- 从 a 到 b 距离为 2
- 从 a 到 c 距离为 5
更新后的距离表:
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| b | 2 (a,b) | ||||
| c | 5 (a,c) | ||||
| d | ∞ | ||||
| e | ∞ | ||||
| f | ∞ | ||||
| 终点集 | {a,b} |
步骤 2:
选择距离最小的节点 b,更新其邻接节点 d 和 c 的距离:
- 从 b 到 d 距离为 5 (2 + 3)
- 从 b 到 c 距离为 3 (2 + 1) → 更新 c 的距离
更新后的距离表:
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| b | 2 (a,b) | ||||
| c | 5 (a,c) | 3 (a,b,c) | |||
| d | ∞ | 5 (a,b,d) | |||
| e | ∞ | ∞ | |||
| f | ∞ | ∞ | |||
| 终点集 | {a,b} | {a,b,c} |
步骤 3:
选择距离最小的节点 c,更新其邻接节点 e 的距离:
- 从 c 到 e 距离为 7 (3 + 4)
更新后的距离表:
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| b | 2 (a,b) | ||||
| c | 5 (a,c) | 3 (a,b,c) | |||
| d | ∞ | 5 (a,b,d) | 5 (a,b,d) | ||
| e | ∞ | ∞ | 7 (a,b,c,e) | ||
| f | ∞ | ∞ | 4 (a,b,c,f) | ||
| 终点集 | {a,b} | {a,b,c} | {a,b,c,f} |
步骤 4:
选择距离最小的节点 f,更新其邻接节点
由于其不可达别的点,所以照搬上次的结果
更新后的距离表:
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| b | 2 (a,b) | ||||
| c | 5 (a,c) | 3 (a,b,c) | |||
| d | ∞ | 5 (a,b,d) | 5 (a,b,d) | 5 (a,b,d) | |
| e | ∞ | ∞ | 7 (a,b,c,e) | 7 (a,b,c,e) | |
| f | ∞ | ∞ | 4 (a,b,c,f) | ||
| 终点集 | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} |
步骤 5:
选择距离最小的节点 d,更新其邻接节点 e 的距离:
- 从 d 到 e 距离为 6 (5 + 1) → 更新 e 的距离
更新后的距离表:
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
| b | 2 (a,b) | ||||
| c | 5 (a,c) | 3 (a,b,c) | |||
| d | ∞ | 5 (a,b,d) | 5 (a,b,d) | 5 (a,b,d) | |
| e | ∞ | ∞ | 7 (a,b,c,e) | 7 (a,b,c,e) | 6 (a,b,d,e) |
| f | ∞ | ∞ | 4 (a,b,c,f) | ||
| 终点集 | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} | {a,b,c,f,d,e} |
最终得出a到其他点的最短路径为:
从 a 到 b 的最短路径:a → b,距离 2
从 a 到 c 的最短路径:a → b → c,距离 3
从 a 到 d 的最短路径:a → b → d,距离 5
从 a 到 e 的最短路径:a → b → d → e,距离 6
从 a 到 f 的最短路径:a → b → c → f,距离 4
1.3 408真题
【2012年】
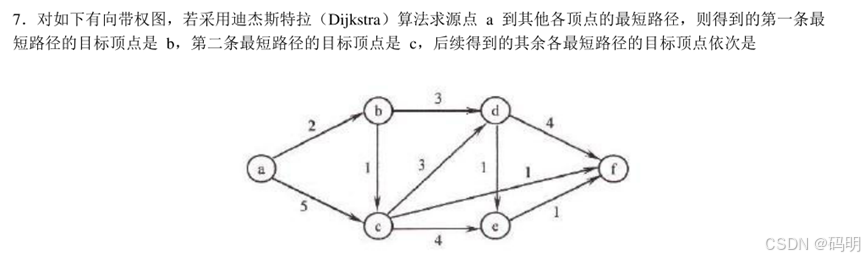
| 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 | |
| b | 2 a→b | ||||
| c | 5 a→c | 3 a→b→c | |||
| d | ∞ | 5 a→b→d | 5 a→b→d | 5 a→b→d | |
| e | ∞ | ∞ | 7 a→b→c→e | 7 a→b→c→e | 7 a→b→c→e |
| f | ∞ | ∞ | 4 a→b→c→f | ||
| 终点集S | {a,b} | {a,b,c} | {a,b,c,f} | {a,b,c,f,d} | {a,b,c,f,d,e} |
答案:f d e
【2016年】
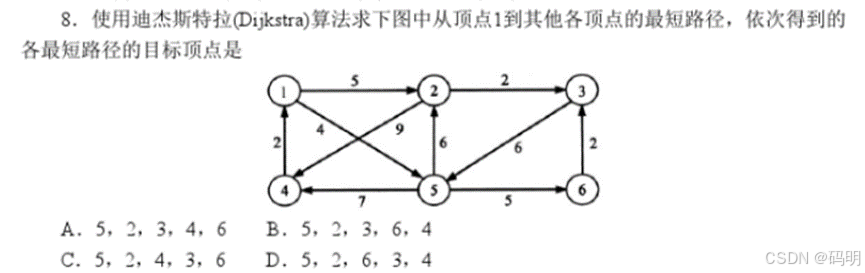
| 第一轮 | 第二轮 | 第三轮 | 第四轮 | 第五轮 | |
| 2 | 5 1→2 | 5 1→2 | |||
| 3 | ∞ | ∞ | 7 1→2→3 | ||
| 4 | ∞ | 11 1→5→4 | 11 1→5→4 | 11 1→5→4 | 11 1→5→4 |
| 5 | 4 1→5 | ||||
| 6 | ∞ | 9 1→5→6 | 9 1→5→6 | 9 1→5→6 | |
| 终点集S | {5} | {5,2} | {5,2,3} | {5,2,3,6} | {5,2,3,6,4} |
答案B
【2021年】
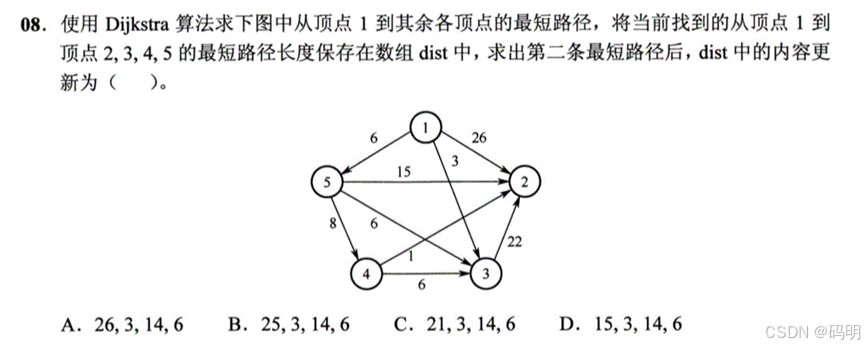
| 第一轮 | 第二轮 | 第三轮 | 第四轮 | |
| 2 | 26 1→2 | 25 1→3→2 | 21 1→5→2 | 15 1→5→4→2 |
| 3 | 3 1→3 | |||
| 4 | ∞ | ∞ | 14 1→5→4 | |
| 5 | 6 1→5 | 6 1→5 | ||
| 终点集S | {3} | {3,5} | {3,5,4} | {3,5,4,2} |
答案:C
1.4 快速解法
根据上面的解题过程可以发现:解出到各点最短路径的次序是根据最短路径的大小升序排列的。
也即:考试时可以打眼看出出发点到各个点的最短路径,接着按从小到达的次序排列就可以找到解出到各点最短路径的次序。
2.Floyd算法【多源最短路径】
2.1步骤
弗洛伊德算法(Floyd-Warshall Algorithm)用于求解图中任意两点之间的最短路径。可以用以下步骤描述它:
- 初始化距离矩阵:首先,你需要创建一个距离矩阵,矩阵的每个元素表示图中两点之间的距离。如果两点之间有边,就填上边的权重;如果没有边,则填上一个很大的数(表示不可达),自己到自己填0。
- 迭代处理每个中间点:接下来,算法会尝试每一个点作为中间点。假设我们要通过某个点(中间点)来优化从点A到点B的路径。对于每一对点A和B,检查通过这个中间点能否找到更短的路径。
- 更新距离:如果通过中间点的路径长度比直接从A到B的距离还短,就更新距离矩阵中的值。也就是说,若dist[A][B] > dist[A][K] + dist[K][B],那么就更新dist[A][B]为dist[A][K] + dist[K][B]。
- 重复:将上一步的过程重复进行,直到所有的点都被用作中间点。
- 最终结果:最后,你的距离矩阵就包含了图中所有点对之间的最短路径长度。可以通过这个矩阵直接得到任意两点之间的最短路径。
这个算法的时间复杂度是O(V^3),其中V是图中点的数量,适合点数相对较少的情况。
2.2实例:
有向图G:
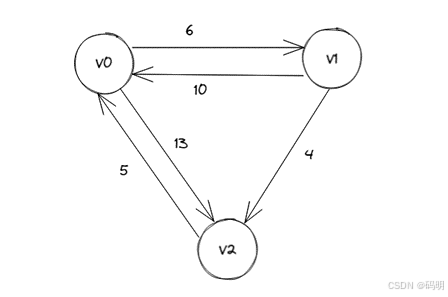
G的邻接矩阵:
| V0 | V1 | V2 | |
| V0 | 0 | 6 | 13 |
| V1 | 10 | 0 | 4 |
| V2 | 5 | ∞ | 0 |
Floyd算法:
1.初始化:
| A(-1) | |||
| V0 | V1 | V2 | |
| V0 | 0 | 6 | 13 |
| V1 | 10 | 0 | 4 |
| V2 | 5 | ∞ | 0 |
2.第一轮:
| A(0) | |||
| V0 | V1 | V2 | |
| V0 | 0 | 6 | 13 |
| V1 | 10 | 0 | 4 |
| V2 | 5 | 11 | 0 |
3.第二轮
| A(1) | |||
| V0 | V1 | V2 | |
| V0 | 0 | 6 | 10 |
| V1 | 10 | 0 | 4 |
| V2 | 5 | ∞ | 0 |
4.第三轮
| A(2) | |||
| V0 | V1 | V2 | |
| V0 | 0 | 6 | 13 |
| V1 | 9 | 0 | 4 |
| V2 | 5 | ∞ | 0 |
此轮矩阵所存储的就是各点之间的最短距离。
3.广度优先遍历,迪杰斯特拉和弗洛伊德算法求最短路径的总结
| BFS | Dijkstra | Floyd | |
| 用途 | 求单源最短路径 | 求单源最短路径 | 求各项点之间的最短路径 |
| 无权图 | 适用 | 适用 | 适用 |
| 有权图 | 不适用 | 适用 | 适用 |
| 带负权值的图 | 不适用 | 不适用 | 适用 |
| 带负权回路的图 | 不适用 | 不适用 | 不适用 |
| 时间复杂度 | O(|v|^2)或O(|v|+|e|) | O(|v|^2) | O(|v|^3) |
