【动手学深度学习】6.1 从全连接层到卷积

• 之前讨论的MLP十分适合处理表格数据，其中行对应样本，列对应特征。
• 对于表格数据我们寻找的模式可能涉及特征之间的交互，此时我们不能预先假设特征之间的交互。这使得多层感知机可能是最好的选择。但是对于高维感知数据，这种缺少结构的网络可能会变得不实用
• 在之前猫狗分类的例子中。数据集是有标注的图片，每张图片为百万级别的像素，这就意味着每次输入的维度都是百万级别的，就算将隐藏层维度降低到1000，这样的参数量也是十分恐怖的 $10^6\times 10^3=10^9$，会导致训练计算量过大
• 如果狠狠压缩分辨率，那么这会导致图像的特征不能被很好的学习，并且拟合如此多的参数还需要大量的数据。
• 而图像中含有很多丰富的结构，这些结构可以被利用到。而CNN就是利用自然图像中一些已知结构的创造新方法

---

1. 不变性

• 假设我们想从一张图片中找到某个物体，那么我们无论用哪种方法找到这种物体，都应该和物体的位置无关
• 在“沃尔多在哪里”的游戏中，要找出沃尔多，那么我们可以将图像分割成多个区域，并为每个区域包含沃尔多的可能性打分
• 卷积神经网络正是将空间不变性这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示
  
• 总结上面的想法，从而帮助我们设计适合于计算机视觉的神经网络架构
  • 平移不变性：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。
  • 局部性： 神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，可以聚合这些局部特征，以在整个图像级别进行预测。

---

2. 多层感知机的限制

• 我们定义输入的二维图像为 X，隐藏表示为 H 上在数学上是一个矩阵，代码上为一个二维张量。
• 为了方便理解，我们认为无论是输入还是隐藏表示都有空间结构
  
• 权重矩阵为何为四维可以用下图来理解：在之前我们是将其展成一个向量，但是在这里我们以二维为输入和输出
  
  
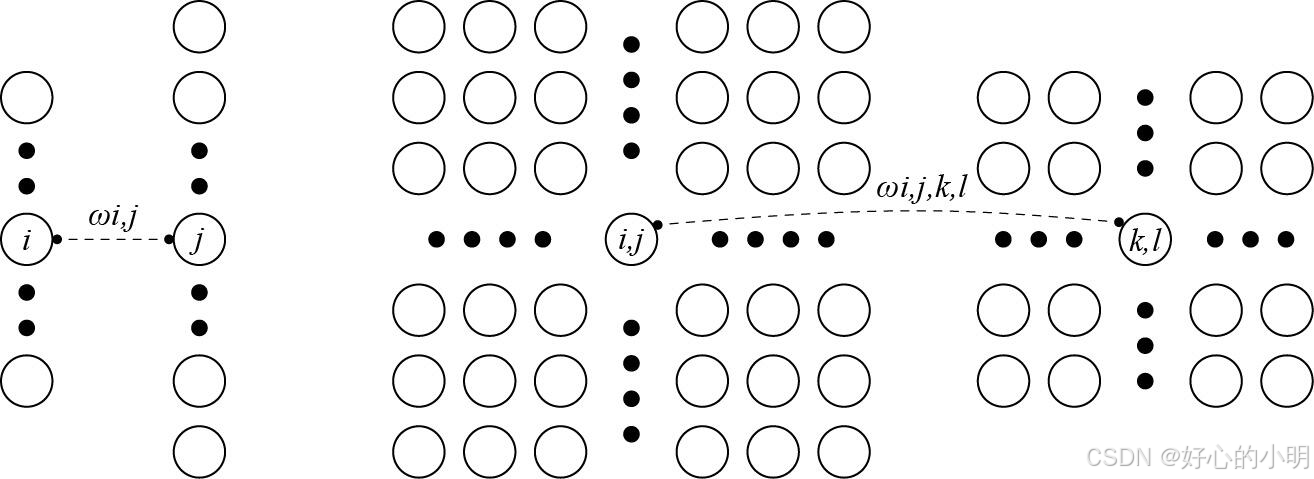
• 对上面这段话的理解：就是对于 $H_{i,j}$ 来说，它的结果是 $X_{i.j}$ 为中心的a，b范围进行加权求和得到的
  

2.1 平移不变性

• 当这个信息换个位置的时候，导致的结果只有结果的位置的变换，所以我们的信息经过平移后内容本身不会改变，而是只改变了输出的位置
  

2.2 局部性

• 只考虑局部的信息，即对局部加权求和，而不是对全局做加权求和
  

---

3. 卷积

---

4. “沃尔多在哪里”回顾

• 回到上面的“沃尔多在哪里”游戏，让我们看看它到底是什么样子。卷积层根据滤波器 V 选取给定大小的窗口，并加权处理图片，如下图中所示。我们的目标是学习一个模型，以便探测出在“沃尔多”最可能出现的地方。
  

4.1 通道

• 上面的方法存在一个问题：图像一般包含三个通道，而我们上面只有二维。固我们的索引应该相应的调整为三维
• 我们的输入是三维的，固我们的隐藏表示也最好是三维的。换句话说就是对于每个空间位置我们采用一组而不是一个隐藏表示。因此，我们可以把隐藏表示为一系列具有二维张量的通道。
• 这些通道有时也被称为特征映射，因为每个通道都向后续层提供一组空间话的学习特征。直观上可以想象在靠近输入的底层，一些通道专门识别边缘，而一些通道专门识别纹理
• 由上，我们的公式就可以变换为