PageRank算法：从原理到实战

在这个信息爆炸的时代，搜索引擎成为了我们获取知识的重要途径。而PageRank算法作为谷歌搜索引擎背后的关键技术之一，其重要性不言而喻。今天，我们就来一起探索一下PageRank算法的魅力所在，并通过一个小实战案例来看看它是如何工作的。

一 算法来源

​ 这个要从搜索引擎的发展讲起。最早的搜索引擎采用的是 分类目录的方法，即通过人工进行网页分类并整理出高质量的网站。那时 Yahoo 和国内的 hao123 就是使用的这种方法。

​ 后来网页越来越多，人工分类已经不现实了。搜索引擎进入了 文本检索 的时代，即计算用户查询关键词与网页内容的相关程度来返回搜索结果。这种方法突破了数量的限制，但是搜索结果不是很好。因为总有某些网页来回地倒腾某些关键词使自己的搜索排名靠前。

​ 在谷歌诞生之前那段时间，流行的网页排名算法都很类似，它们都使用了一个非常简单的思想：越是重要的网页，访问量就会越大，许多大公司就通过统计网页的访问量来进行网页排名。但是这种排名算法有两个很显著的问题：

​ 1. 因为只能够抽样统计，所以统计数据不一定准确，而且访问量的波动会比较大，想要得到准确的统计需要大量的时间和人力，还只能维持很短的有效时间。

​ 2. 访问量并不一定能体现网页的“重要程度”，可能一些比较早接触互联网的网民还记得，那时有很多人推出了专门“刷访问量”的服务。

​ 那有没有更好的方法，不统计访问量就能够为网页的重要度排序呢？

​ 于是我们的主角要登场了。没错，谷歌的两位创始人，当时还是美国斯坦福大学 (Stanford University) 研究生的佩奇 (Larry Page) 和布林 (Sergey Brin) 开始了对网页排序问题的研究。他们的借鉴了学术界评判学术论文重要性的通用方法， 那就是看论文的引用次数。由此想到网页的重要性也可以根据这种方法来评价。于是PageRank的核心思想就诞生了，非常简单：

• 如果一个网页被很多其他网页链接到的话说明这个网页比较重要，也就是PageRank值会相对较高
• 如果一个PageRank值很高的网页链接到一个其他的网页，那么被链接到的网页的PageRank值会相应地因此而提高

就如下图所示（一个概念图）:

二 模拟PageRank算法的运行过程

​ 在详细讲述这个算法之前，不妨让我们用一个游戏，先来简单模拟一下PageRank算法的运行过程，以便读者更好地理解。

​ 三兄弟分30颗豌豆，起初每人10颗，他们每次都要把手里的豌豆全部平均分给自己喜欢的人，下图表示了三兄弟各自拥有的初始豌豆数量，以及相互喜欢的关系（箭头方向表示喜欢，例如老二喜欢老大，老大喜欢老二和老三）。

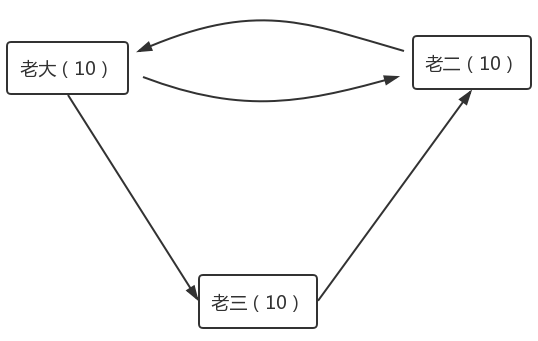
​ 第一次分配后，我们会得到结果如下：

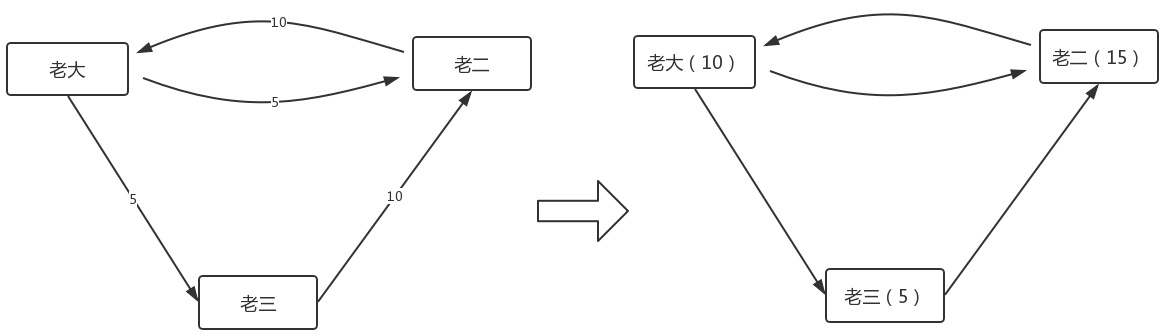
​ 就这样，让游戏一直进行下去，直到他们手中的豌豆数不再变化为止。

​ 那么这个游戏到底是否可以结束呢，如果可以，最终的结果又是什么样的？

​ 在此我们用电脑模拟了这个过程，得出的结果是：老大和老二的盘子里各有12颗豌豆，而老三的盘子里有6颗豌豆，这时候无论游戏怎么进行下去，盘子里的豌豆数量都不会再变化。

​ 看到这里，读者可能会问：这个游戏和网页排序有什么关系？

​ 实际上，PageRank会给每个网页一个数值，这个数值越高，就说明这个网页越“重要”。

​ 而刚刚的游戏中，如果把豌豆的数量看作这个数值（可以不是整数），把孩子们看作网页，那么游戏的过程就是PageRank的算法，而游戏结束时豌豆的分配，就是网页的PageRank值。

三 简单PageRank算法

首先，将Web做如下抽象：

• 将每个网页抽象成一个节点；
• 如果一个页面A有链接直接链向B，则存在一条有向边从A到B（多个相同链接不重复计算边）。

因此，整个Web被抽象为一张有向图。现在假设世界上只有四张网页：A、B、C、D，其抽象结构如下图：

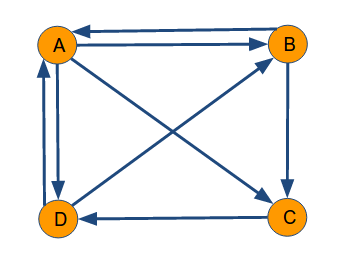
显然这个图是强连通的（从任一节点出发都可以到达另外任何一个节点）。然后需要用一种合适的数据结构表示页面间的连接关系。

PageRank算法基本思想描述：被用户访问越多的网页更可能质量越高，而用户在浏览网页时主要通过超链接进行页面跳转，因此需要通过分析超链接组成的拓扑结构来推算每个网页被访问频率的高低。最简单的，我们可以假设当一个用户停留在某页面时，跳转到页面上每个被链页面的概率相同。

对任意一个网页P：

$I(P)$ : 表述其重要性，并称之为网页的网页排序，即排序的分值。

假定网页 $P_j$ 有 $l_j$ 个链接，如果这些 $l_j$ 个链接中的一个链接到网页 $P_i$ ,那么网页 $P_j$ 会将其重要性的 $\frac{1}{l_j}$ 赋值给 $P_i$ 。网页 $P_i$ 的重要性就是所有指向这个网页的其它网页所贡献的重要性的加和。换言之，如果我们记链接到网页 $P_i$ 的网页集合为 $B_i$ ,那么
$$I(P_i)=\sum _{P_j\in B_i}\frac{I(P_j)}{l_j}$$
​ 这或许会让你想起 “先有鸡还是先有蛋” 的问题：为了确定一个网页的重要性，我们首先得得知所有指向它的其它网页的重要性。然而，我们可以将这个问题改写成一个更数学化的问题。

​ 首先，建立一个矩阵，称为超链矩阵 （hyperlink matrix）,$M=[M_{ij}]$ ,其中第 $i$ 行第$j$ 列的元素为：
$$M_{ij}=\{\begin{array}{ll}1/l_j& \text{if Pj∈Bi }\\ 0& \text{otherwise}\end{array}$$
例如，上图中A页面链向B、C、D，所以一个用户从A跳转到B、C、D的概率各为1/3。设一共有N个网页，则可以组织这样一个N维矩阵，其中第i行j列的值表示用户从页面j转到页面i的概率。这样一个矩阵叫做转移矩阵（Transition Matrix）。下面是上图的转移矩阵M：
$$M=\left[\begin{array}{cccc}0& 1/2& 0& 1/2\\ 1/3& 0& 0& 1/2\\ 1/3& 1/2& 0& 0\\ 1/3& 0& 1& 0\end{array}\right]\text{\hspace{1em}(1)}$$
设初始时每个页面的$rank$值为$1/N$，这里就是$1/4$。按$A-D$顺序得到向量$v$：
$$v=\left[\begin{array}{c}1/4\\ 1/4\\ 1/4\\ 1/4\end{array}\right]\text{\hspace{1em}(2)}$$

**注意：**M第一行分别是A、B、C和D转移到页面A的概率，而v的第一列分别是A、B、C和D当前的rank，因此用M的第一行乘以v的第一列，所得结果就是页面A最新rank的合理估计，同理，Mv的结果就分别代表A、B、C、D新rank值。

然后用M再乘以这个新的rank向量，又会产生一个rank向量。迭代这个过程，可以证明v最终会收敛，即v≈Mv，此时计算停止。最终的v就是各个页面的pagerank值。上面的向量经过几步迭代后，大约收敛在**（1/4,1/4,1/5,1/4），这就是A、B、C、D最后的pagerank**。

四 终止点问题

上面过程要满足收敛性，需要具备一个条件：图是强连通的，即从任意网页可以到达其他任意网页。

互联网中存在网页不满足强连通的特性，因为有一些网页不指向任何网页，按照上面公式迭代计算下去，导致前面累计得到的转移概率被清零，最终得到的概率分布向量所有元素几乎都为0。

假设把上面图中C到D的链接丢掉，C变成了一个终止点，得到下面这个图：

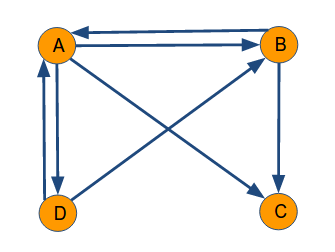
转移矩阵M为：
$$M=\left[\begin{array}{cccc}0& 1/2& 0& 1/2\\ 1/3& 0& 0& 1/2\\ 1/3& 1/2& 0& 0\\ 1/3& 0& 0& 0\end{array}\right]\text{\hspace{1em}(4)}$$
不断迭代，最终得到所有元素都为0。

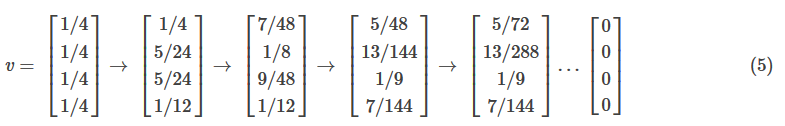
五 陷阱问题

陷阱问题：是指有些网页不存在指向其他网页的链接，但存在指向自己的链接。比如下面这个图：

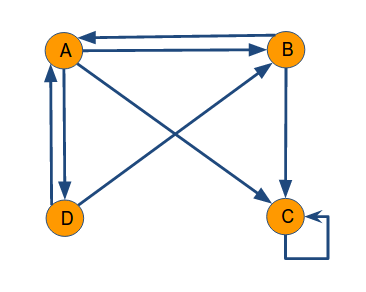
这种情况下，PageRank算法不断迭代会导致概率分布值全部转移到c网页上，这使得其他网页的概率分布值为0，从而整个网页排名就失去了意义。如果按照上面图则对应的转移矩阵M为：

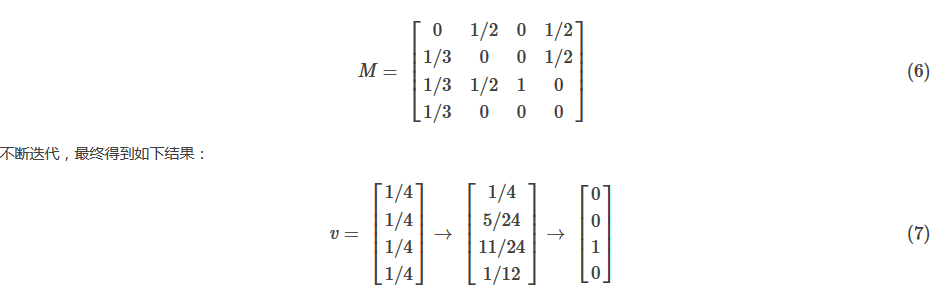
为了解决终止点问题和陷阱问题，下面需要对算法进行改进。假设选取下一个跳转页面时，既不选当前页面，也不选当前网页上的其他链接，而是以一定概率跳转到其他不相关网页，那么上面两个问题就能得到很好的解决，这就是完整PageRank算法思想。

假设跳转到当前页面（包括当前页面上的链接）的概率为a（也称为基尼系数），那么跳转到其他页面概率为(1−a)，进一步假设每个页面被访问的概率相同都是1/n，于是原来的迭代公式转化为:
$$v^{{}^{\prime }}=\alpha Mv+(1-\alpha )e\text{\hspace{1em}(8)}$$
假设α的值为0.85，e是网页数目的倒数，共4个网页，所以e等于1/4。现在计算有陷阱的网页的概率分布：

利用上面公式继续迭代下去，直到收敛，得到最终rank值。

六 Spark实现RageRank

这里简化初始值为1.0，α/N设置为0.15，迭代次数参考《数学之美》中提到：“一般来讲，只要10次左右的迭代基本上就收敛了”，这里设置为10次。

// 生成网页边的关系
val links = sc.parallelize(Array(('A',Array('D')),('B',Array('A')),('C',Array('A','B')),('D',Array('A','C'))),2).map(x => (x._1, x._2)).cache()// 初始化rank值，2表示分两个partition
var ranks = sc.parallelize(Array(('A',1.0),('B',1.0),('C',1.0),('D',1.0)), 2)// 迭代10次
for ( i <- 1 to 10){val contribs = links.join(ranks, 2)val flatMapRDD = contribs.flatMap {case (url,(links,rank)) => links.map(dest => (dest, rank/links.size))}val reduceByKeyRDD = flatMapRDD.reduceByKey(_ + _, 2)ranks = reduceByKeyRDD.mapValues(0.15 + 0.85 * _)
}