当前位置：首页 > news >正文

力扣题解2576

news 2025/5/9 9:15:25

大家好，欢迎来到无限大的频道。

今日继续给大家带来力扣题解。

题目描述：

给你一个下标从 0 开始的整数数组 nums 。

一开始，所有下标都没有被标记。你可以执行以下操作任意次：

选择两个互不相同且未标记的下标 i 和 j ，满足 2 * nums[i] <= nums[j] ，标记下标 i 和 j 。

请你执行上述操作任意次，返回 nums 中最多可以标记的下标数目。

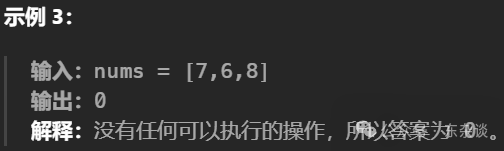
解题思路：

算法的核心思路是：

对数组进行排序。
使用双指针的方式遍历排序后的数组，寻找符合条件的下标。
每当找到一对符合条件的下标时，就将它们标记

分析题目和示例，我们以更深刻地理解下标标记的逻辑。原先整数数组的下标在被标记的之后，只是数据被标记，而非其固定的位置被标记，也就是说，是因为这个数据符合条件，从而标记该位置，而不是因为该位置符合条件，而去标记数据。

题目的关键在于标记的是数组中元素的特性，而非其在数组中的位置固定性。（这个是我个人总结出来的，在很多的算法问题中都有所体现）

所以当大家理解了这个条件之后，就可以把原先的数组进行排序，从而简化问题。

排序的经典函数如下

int compare(const void *a, const void *b) {return (*(int *)a - *(int *)b);
}

之后便是在解决问题的函数中进行调用

    qsort(nums, numsSize, sizeof(int), compare);

在这之后，我们的数组num，就变成了一个非递减排列的数组。

排序之后，就是采用双指针遍历数组了（因为涉及两个变量的比较，所以我采用了双指针的方式）

int compare(const void *a, const void *b) {return (*(int *)a - *(int *)b);
}

int maxMarkableIndices(int* nums, int size) {// 先对数组进行排序qsort(nums, size, sizeof(int), compare);int markedCount = 0;     // 标记的下标数量int i = 0;                // 指向较小数字的指针int j = 0;                // 指向较大数字的指针
// 使用双指针遍历数组while (i < size && j < size) {// 找到一对符合条件的 (i, j)if (2 * nums[i] <= nums[j] && i != j) {markedCount += 2; // 每找到一对就标记两个下标i++;              // 移动指针 ij++;              // 移动指针 j} else {// 如果不符合条件，移动 j 指针j++;}// 如果 j 指针已经达到数组的末尾，上面条件再检查时需要重置 j，给下一个 i 对应的 jif (j == size && i < size) {j = i + 1; // 对下一个 i 找 j}}
return markedCount; // 返回最多可以标记的下标数量
}
//双指针：使用两个指针 i 和 j，
//其中 i 指向较小的元素，j 指向较大的元素。
//每当找到符合条件的 (i, j) 对时，就将 markedCount 增加 2，
//并移动两个指针

但是写完之后发现，这个代码的时间复杂度过高，不在题目的考虑范围之内，所以在此基础上继续优化。

在长度为 n 的数组当中，最理想的情况下只会产生 n/2 个下标数目，因为题目要求“互不相同且未标记”

由此对数组进行排序后，我们将其一分为二，左侧的元素只与右侧的元素进行匹配，其余思路同上，得出代码

int compare(const void* a, const void* b) {return (*(int*)a - *(int*)b);
}

int maxNumOfMarkedIndices(int* nums, int numsSize){qsort(nums, numsSize, sizeof(int), compare);int n = numsSize;int m = n / 2;int res = 0;for (int i = 0, j = m; i < m && j < n; i++) {while (j < n && 2 * nums[i] > nums[j]) {j++;}if (j < n) {res += 2;j++;}}return res;
}