遍历结果的推导

 可以使用的递归思想，但是也可以使用以下“仙术”

在做习题时，常常会遇到下列相关的问题，这些问题可以很好的帮助并丰富对二叉树数据结构的整体框架：

已知前/后序遍历，中序遍历，求后/前序遍历

已知前序遍历：我们可以得到前序遍历的第一个节点就是根节点；

已知后序遍历：我们可以得到后序遍历的最后一个节点是根节点；

示例1：

已知：
前序遍历是：ABCDEFG

中序遍历是：CBEDAFG

我们可以使用一种巧妙地方法：(表格分区)

1. 对于已知前中序遍历结果，求后序遍历的结果：
2. 对于前序遍历，竖直方向，从上到下，依次填入节点；
3. 对于中序遍历，水平方向，从左到右，依次填入节点；
4. 水平轴与竖直轴依次对应，两两相同的进行对应节点的填入；
5. 找到最高的节点（根节点），左边为左子树，右边为右子树；
6. 请他节点的连接与5.类似；

图形展示：

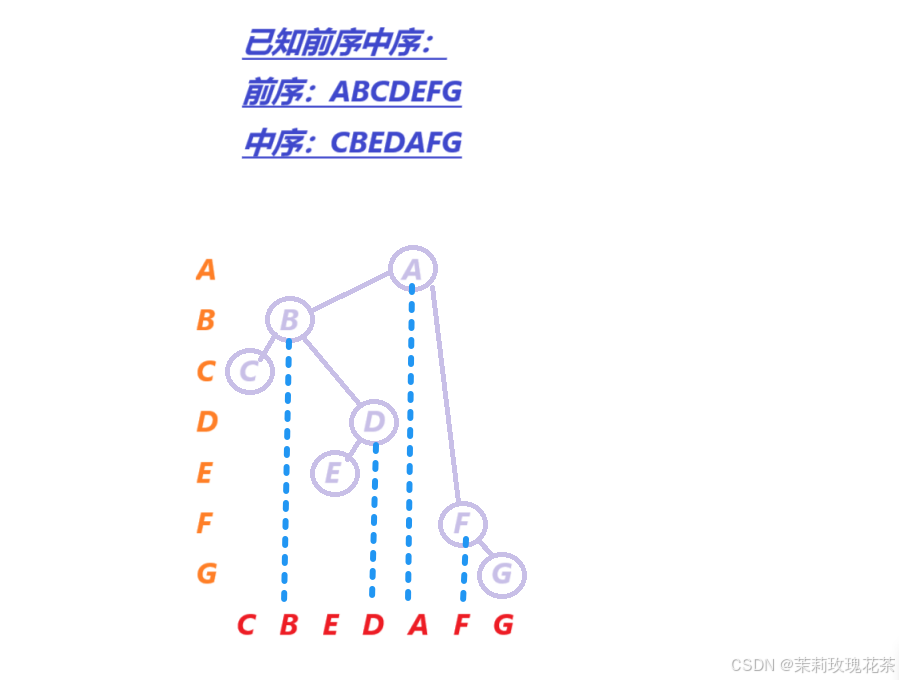
这样，我们就可以得到二叉树的本身，在用后序遍历的思想，便可以得出：

后序遍历：CEDBGFA

示例2：

已知：
后序遍历是：CEDBGFA

中序遍历是：CBEDAFG

步骤：

1. 对于已知后中序遍历结果，求前序遍历的结果：
2. 对于后序遍历，竖直方向，从下到上，依次填入节点；
3. 对于中序遍历，水平方向，从左到右，依次填入节点；
4. 水平轴与竖直轴依次对应，两两相同的进行对应节点的填入；
5. 找到最高的节点（根节点），左边为左子树，右边为右子树；
6. 请他节点的连接与5.类似；

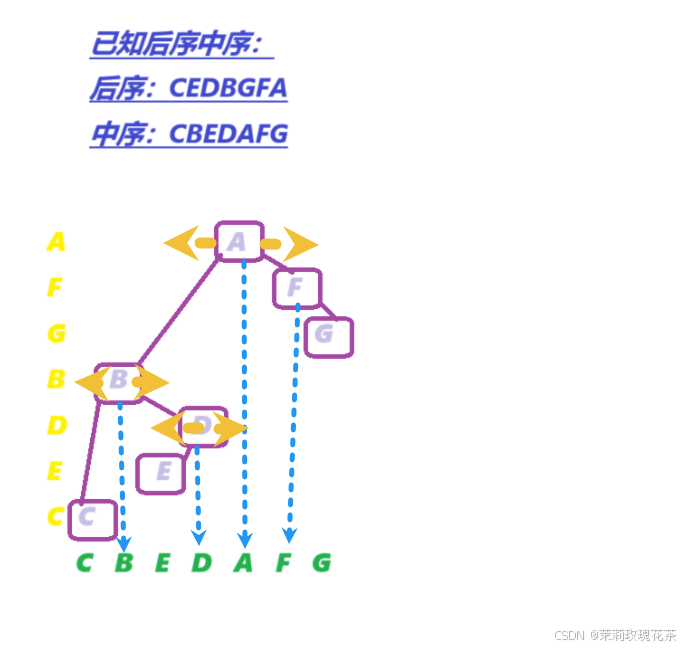
这样，我们就可以得到二叉树的本身，在用后序遍历的思想，便可以得出：

前序遍历：ABCDEFG

下面，我们来看一下更多的数据：

已知：

后序遍历是：JGKHDBLMIEFCA 

中序遍历是：JGDHKBAELIMCF

效果展示：

 

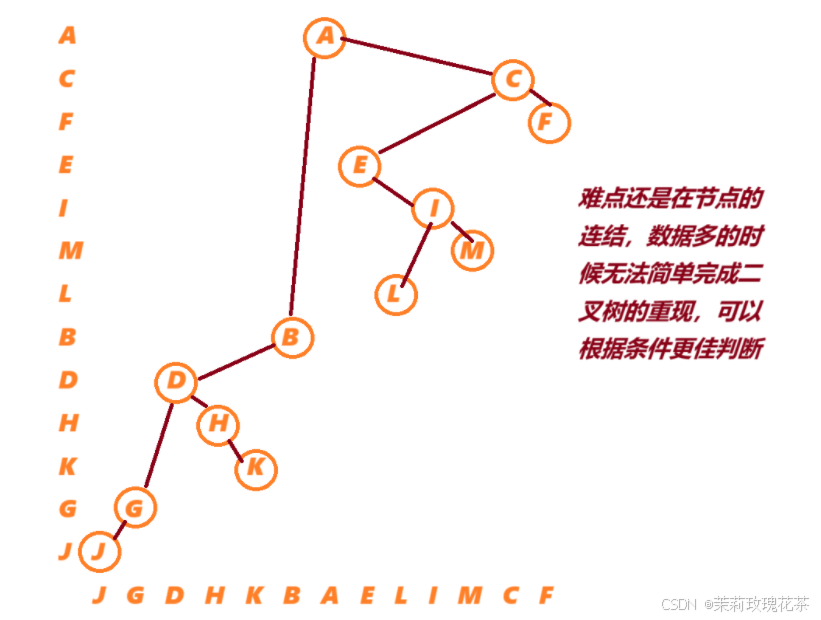
这样，我们就可以得到二叉树的本身，在用后序遍历的思想，便可以得出：

前序遍历：ABDGJHKCEILMF

还有一种题型是树的计数问题：

示例：

如果一颗二叉树的前序遍历的结果是ABCD，则满足条件的不同的二叉树有（ ? ）种

这道题综合考察了二叉树的遍历还有卡特兰数的相关知识点，想要弄懂这道题，我们需要从两个方面入手：

• 先序遍历和中序遍历的关系

我们可以根据先序遍历和中序遍历，可以重建出唯一的二叉树，所以，在我们知道一颗二叉树的前序遍历的结果是ABCD，想要知道满足条件的不同的二叉树有多少种时，我们就还应该知道这些二叉树的中序遍历的结果有多少，就是以先序遍历作为入栈条件，以不同的出栈，出的结果就是不同的中序遍历：（例子）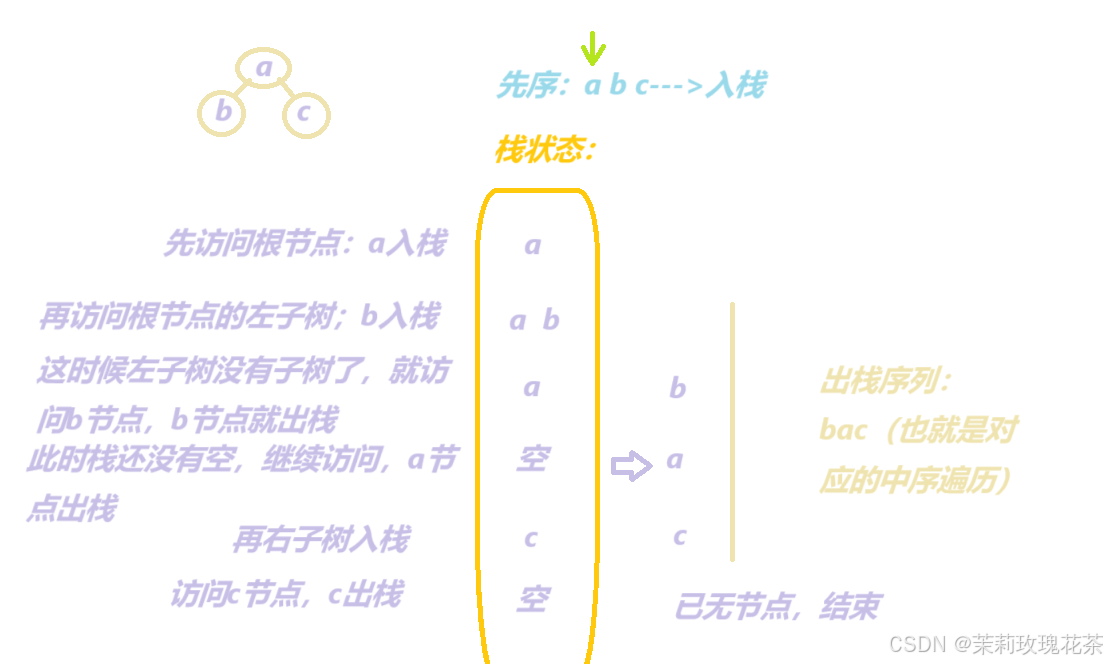

所以，我们可以将问题转换为：把a,b,c,d按照顺序入栈，可以得到多少种出栈序列

• 运用卡特兰数来确定出栈序列的个数

卡特兰数的式子：

怎么得到这个式子呢？

我们把入栈视为+1，出栈视为-1

n=3的入栈序列对应的出·入栈序列为2n=6

比如：

+1 +1 +1 -1 -1 -1：连续入栈3次，再连续出栈3次

但是，其实所有合法的序列，他的前缀和是要>=0的，栈里是要有元素才可以出栈

比如：

+1 -1 -1 +1 +1 -1：前三个的前缀和就<0了

这就是在栈空的情况下还进行出栈操作，这显然是不合法的

 那么我们有多少个不合法的，我们要解决这个问题就需要找到第一个前缀和<0的位置，把位置前的所有的数据(包括位置上的数据)进行按位取反（对应上面不合法的例子）

-1 +1 +1 +1 +1 -1：”按位取反“结果

对于每一个非法序列，都有唯一一个对应的序列，总的非法个数就是在2n的长度中，放入n+1个+1，也就对应这组合个数：

总的非法+合法个数就是在2n的长度中，放入n个+1，也就对应这组合个数：

所以，就可以得到对应的式子了

所以，本题就可以得到解决：answer=